About Differential Equation Solvers
Ordinary Differential Equation (ODE) solvers solve an equation or system of equations for unknown functions of one variable. Partial Differential Equation (PDE) solvers solve for functions of two variables (1D PDEs).
Ordinary Differential Equations
To solve an ODE directly without creating a solve block, use one of the ODE solvers, which solve systems of ODEs of the following form:
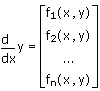
where y is vector of unknown functions of the independent variable x. To solve a higher-order ODE, rewrite it as a system of first order ODEs.
The ODE solvers are divided into two types: solvers for stiff systems and solvers for nonstiff systems. A system of ODEs written in matrix form as y’=Ay, is called stiff if the matrix A is nearly singular. Otherwise, the system is nonstiff.
• Adams—Adams-Bashford methods
• rkfixed, Rkadapt, Bulstoer—4th order Runge Kutta method, with fixed and adaptive step size, and Bulstoer method for smoothly varying ODEs
• BDF—Backward differentiation formula methods
• Radau, Stiffb, Stiffr—RADAU, Bulirsch-Stoer, and Rosenbrock methods for stiff systems
• statespace—Systems of linear, first-order ODEs
• bvalfit, sbval—Boundary-value problems, where not all initial conditions are known, converted to initial value problems by linear shooting
There are also a variety of special polynomial generators and hypergeometric functions which solve specific, common ODEs.
Partial Differential Equations
• numol—Command-line solver for hyperbolic and parabolic systems of 1D PDEs, including coupled ODEs and algebraic constraints
• relax, multigrid—Command-line solvers for Poisson's/Laplace's elliptic PDE
The numol and multigrid solvers are not interchangeable because they deal with different physics and spatial dimensions.
• numol is intended for solving transient 1D hyperbolic and parabolic PDEs (functions of x,t).
• multigrid is intended for solving steady-state 2D elliptic PDEs (functions of x,y) over a square.
Jacobian
• Jacob —Returns the Jacobian matrix of a vector.