State Space ODE Solver
• statespace(init, t1, t2, intvls, A, [B, u])—Returns the solution to a system of linear, first order ordinary differential equations of the following form:
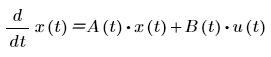
where
◦ x(t)
is a vector of unknown states.
◦ A(t)
is the coupling, or state matrix between the functions in the vector x(t).
◦ B(t)
is an input matrix that describes the coupling between terms in the input vector u(t).
◦ u(t) is the input vector.
The function returns an (intvls+1)×(n+1) solution matrix, where n is the number of unknown states. The first column of the matrix contains the values of t at which the solutions are evaluated. These values are (intvls+1) evenly spaced numbers between t1 and t2. The remaining columns contain the values of the solutions x0, x1, ..., xn-1 corresponding to the values of t in the first column.
Arguments
• init is a column vector of initial conditions, whose length is the number of unknown states.
• t1 is a real number specifying the starting point of the integration interval.
• t2 is a real number specifying the ending point of the integration interval.
• intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
• A is an n × n matrix function of the form A(t), where n is the number of unknown states. The entries of A(t) are functions of the independent variable t.
• B (optional) is an n × k matrix or vector function of the form B(t), whose entries are functions of t.
• u (optional) is a k × 1 vector or real scalar function of the form u(t), whose entries are functions of t.
u is required if you provide the argument B.
• x (optional) is a k × 1 vector or real scalar function of the form x(t), whose entries are functions of t.
x is required if you provide the argument A.
Additional Information
This notation, in which x(t) represents a vector of unknowns for the independent variable t, differs from the notation used in the Help pages for the other ODE solvers, in which the letter x represents the independent variable and y(x) represents the vector of unknowns.