Example: Augmented Jacobian for Stiffb and Stiffr
Use the Jacob function to compute the augmented Jacobian matrix for an ordinary differential equation (ODE), and then provide it as input to solvers Stiffb and Stiffr.
1. Define a system of four unknowns:
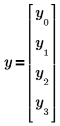 |
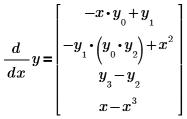 |
|
|
The yi variables are functions of x.
|
2. Define the constants in the system.
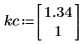 |
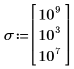 |
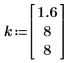 |
3. Define the initial values.
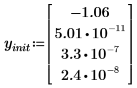
4. Define a vector function D(x,y) corresponding to the right-hand side of the system.
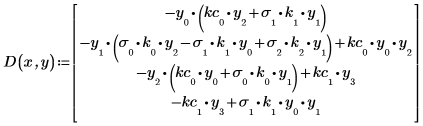
5. Use the augment function to create the augmented Jacobian:
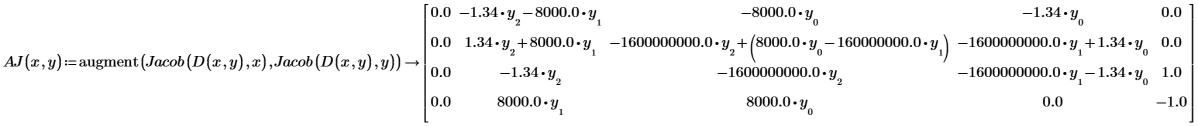
6. Call the Stiffb and Stiffr functions:
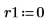 | 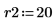 | 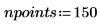 |
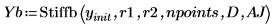 | ||
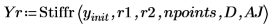 | ||
The returned matrices contain 5 columns corresponding to the number of points and the solutions for the four unknowns. |
7. Extract the solutions for the four unknowns from the returned Stiffb and Stiffr matrices:
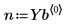 | |
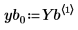 | 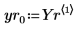 |
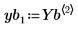 | 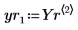 |
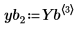 | 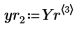 |
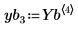 | 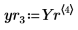 |
8. Plot and compare the returned solutions for each unknown from the two functions:
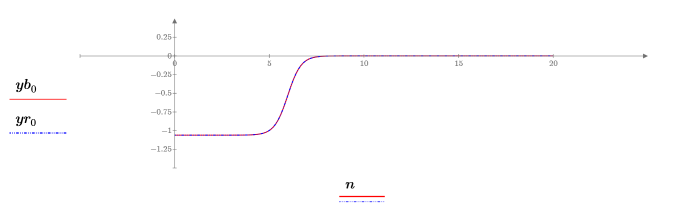
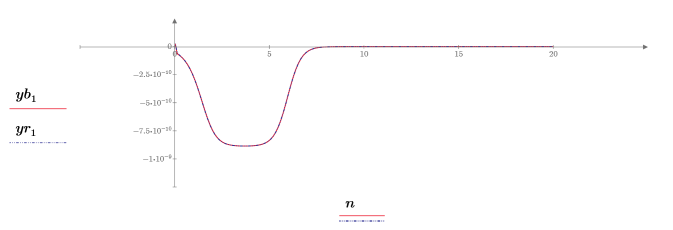
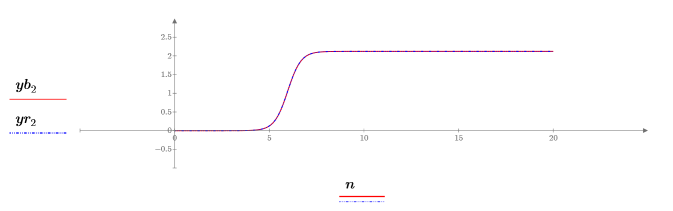
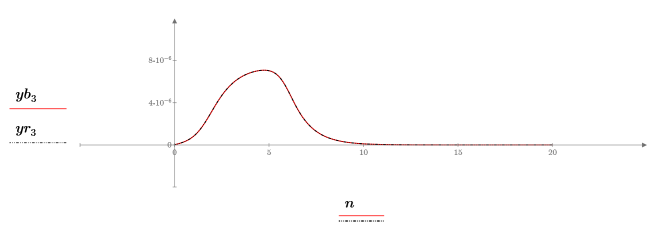
The plots show that the two ODE solvers return identical solutions.