So werten Sie Integrale symbolisch aus
1. Fügen Sie den Operator für Integrale ein.
2. Geben Sie den Ausdruck in den Platzhalter rechts neben dem Integralzeichen ein.
3. Geben Sie die Integrationsvariable x in den Platzhalter rechts neben dem Symbol d ein.
4. Fügen Sie den symbolischen Auswertungsoperator ein.
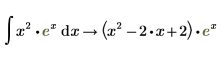
Mit dem symbolischen Auswertungsoperator können Sie nur das unbestimmte Integral auswerten. |
5. Um das bestimmte Integral der gleichen Funktion von 0 bis 5 zu ermitteln, geben Sie 0 in den unteren Platzhalter des Integrals ein. Geben Sie 5 in den oberen Platzhalter ein und wiederholen Sie die Schritte 2 bis 4.
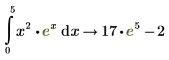
6. Um das bestimmte Integral derselben Funktion zu ermitteln, wenn mindestens einer der Grenzwerte eine undefinierte Variable ist, wiederholen Sie die Schritte 2 bis 4. Fügen Sie dann den unteren und oberen Grenzwert des Integrals ein.
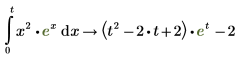
Beim Auswerten eines bestimmten Integrals, in dem mindestens einer der Grenzwerte nicht definiert ist, geht das Symbolik-Modul davon aus, dass der obere Grenzwert größer als der untere Grenzwert ist.
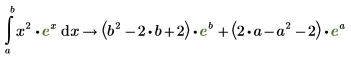
7. Um einer Funktion Ergebnisse der symbolischen Auswertung zuzuweisen, definieren Sie eine Funktion wie folgt:
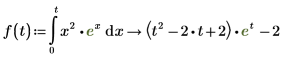
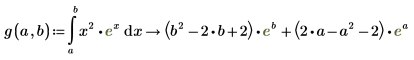
Cauchy-Hauptwert
Der Cauchy-Hauptwert des Integrals um einen Punkt c im Intervall (a,b) wird mit dem folgenden Ausdruck definiert:
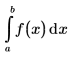
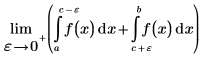
Der Zweck des Cauchy-Hauptwerts ist es, den Wert des Integrals zu definieren, wenn die Funktion f einen Singularitätspunkt bei c aufweist. Das folgende Integral hat z.B. einen Singularitätspunkt bei c=0, und die symbolische Auswertung gibt einen Fehler zurück.
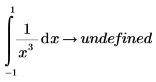
Um den Cauchy-Hauptwert des Integrals zu finden, fügen Sie den Modifizierer cauchy hinzu.
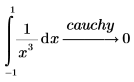
Symbolische Auswertungen von Integralen, die eine Cauchy-Analyse erfordern, geben das Ergebnis undefined zurück, wenn das Schlüsselwort cauchy nicht angegeben wird. |