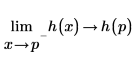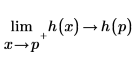Beispiel: Symbolische Analysis I

Symbolische Mathematik > Arbeiten mit symbolischer Mathematik > Analysis > Beispiel: Symbolische Analysis I

Lösen Sie symbolische Probleme in der Analysis, indem Sie den Ausdruck für das Problem mit dem symbolischen Auswertungsoperator auswerten und Schlüsselwörter hinzufügen, um das Problem ggf. zu ändern.

Ableitungen und Integrale

1. Suchen Sie die Ableitung eines Ausdrucks, der die Funktion atan enthält.

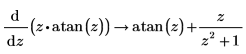
2. Weisen Sie das Ergebnis einer symbolischen Differenziation einer Funktion zu. Dies ist nützlich, wenn nicht für alle Variablen Werte vorhanden sind.

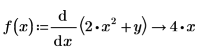
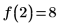
3. Ermitteln Sie die Ableitung der Funktion sin mit einem komplexen Argument.

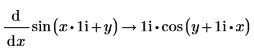
4. Zeigen Sie das Ergebnis mit dem Schlüsselwort rectangular im Standardformat a+bi an.

<region id="ID0EKUHMB" actualWidth="554.50500000000011" actualHeight="53.743333445231123" top="288.00000000000006" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="22">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
            <apply>
              <plus />
              <apply>
                <mult />
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
                <imag symbol="i">1</imag>
              </apply>
              <id xml:space="preserve">y</id>
            </apply>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <id xml:space="preserve">rectangular</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <div />
            <apply>
              <mult />
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="CONSTANT">e</id>
                      <apply>
                        <neg />
                        <parens>
                          <apply>
                            <mult />
                            <real>2</real>
                            <id xml:space="preserve" labels="VARIABLE">x</id>
                          </apply>
                        </parens>
                      </apply>
                    </apply>
                  </apply>
                  <real>1</real>
                </apply>
              </parens>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">sin</id>
                <id xml:space="preserve" labels="*">y</id>
              </apply>
            </apply>
            <apply>
              <mult />
              <real>2</real>
              <apply>
                <pow />
                <id xml:space="preserve" labels="CONSTANT">e</id>
                <apply>
                  <neg />
                  <id xml:space="preserve" labels="VARIABLE">x</id>
                </apply>
              </apply>
            </apply>
          </apply>
          <apply>
            <mult />
            <apply>
              <div />
              <apply>
                <plus />
                <apply>
                  <mult />
                  <apply>
                    <id xml:space="preserve" labels="FUNCTION">cos</id>
                    <id xml:space="preserve" labels="*">y</id>
                  </apply>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="CONSTANT">e</id>
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <real>2</real>
                          <id xml:space="preserve" labels="VARIABLE">x</id>
                        </apply>
                      </parens>
                    </apply>
                  </apply>
                </apply>
                <apply>
                  <id xml:space="preserve" labels="FUNCTION">cos</id>
                  <id xml:space="preserve" labels="*">y</id>
                </apply>
              </apply>
              <apply>
                <mult />
                <real>2</real>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="CONSTANT">e</id>
                  <apply>
                    <neg />
                    <id xml:space="preserve" labels="VARIABLE">x</id>
                  </apply>
                </apply>
              </apply>
            </apply>
            <imag symbol="i">1</imag>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

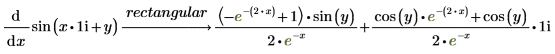
5. Ermitteln Sie das unbestimmte Integral einer Funktion.

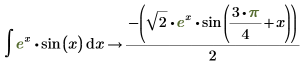
6. Werten Sie das Integral durch Festlegen der Integrationsgrenzen aus.

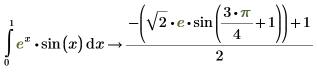
7. Werten Sie das Integral numerisch aus.

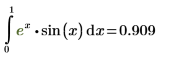
8. Verwenden Sie das Schlüsselwort float, um die Ergebnisse mit größerer Genauigkeit anzuzeigen.

<region id="ID0EO1HMB" actualWidth="433.54333333333335" actualHeight="58.952000000000005" top="633.60000000000014" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="26">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">x</id>
          </boundVars>
          <apply>
            <mult />
            <apply>
              <pow />
              <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">e</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
            </apply>
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">sin</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">x</id>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <real>1</real>
        </upperBound>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">float</id>
          <real>30</real>
        </sequence>
      </command>
      <symResult>
        <real>0.909330673631478617034602154687</real>
      </symResult>
    </symEval>
  </math>
</region>

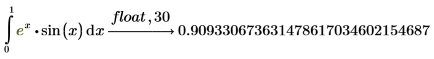
9. Werten Sie Ausdrücke aus, die Parameter im Integrand oder in den Integrationsgrenzen enthalten.

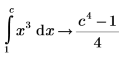
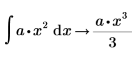
10. Werten Sie ein parametrisiertes Integral aus, das sich unter bestimmten Bedingungen als endlich verhält.

<region id="ID0EK5HMB" actualWidth="199.36333333333332" actualHeight="58.952000000000005" top="979.20000000000016" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <integral />
        <lambda>
          <boundVars>
            <id xml:space="preserve">t1</id>
          </boundVars>
          <apply>
            <pow />
            <id xml:space="preserve" labels="CONSTANT" label-is-contextual="true">e</id>
            <apply>
              <mult />
              <apply>
                <neg />
                <id xml:space="preserve">c</id>
              </apply>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">t1</id>
            </apply>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <id xml:space="preserve" labels="CONSTANT">∞</id>
        </upperBound>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">assume</id>
          <apply>
            <greaterThan />
            <id xml:space="preserve">c</id>
            <real>0</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <real>1</real>
          <id xml:space="preserve" labels="*">c</id>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

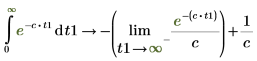
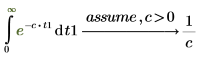
11. Zeigen Sie, dass PTC Mathcad den Hauptsatz der Differential- und Integralrechnung versteht, der die folgenden Beziehungen zwischen Ableitungen und Integrale festlegt:

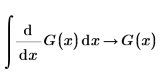
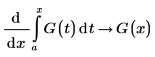
Grenzwerte

1. Werten Sie die Grenzwerte des folgenden Ausdrucks aus:

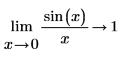
2. Berechnen Sie die links- und rechtsseitigen Grenzwerte von h(x).

Zugehörige Themen

Symbolische Analysis

War dies hilfreich?