Partielle Differentialgleichungen in Lösungsblöcken
pdesolve(u, x, xrange, t, trange, [xpts], [tpts]) – Gibt eine Funktion oder einen Funktionsvektor u(x,t) zurück, der eine eindimensionale nichtlineare partielle Differentialgleichung (Partial Differential Equation, PDE) oder ein System von PDEs mit n unabhängigen Gleichheitsnebenbedingungen für eine Differentialgleichung der n-ten Ordnung löst. Werte werden aus einer Matrix von Lösungspunkten interpoliert, die mit der numerischen Linienmethode berechnet wird.
Sie müssen pdesolve in einem Lösungsblock verwenden.
Argumente
• u ist ein skalarer Funktionsname oder ein Vektor aus Funktionsnamen (ohne Variablennamen), wie sie im Lösungsblock angezeigt werden. Wenn Sie z.B. die Funktionen f(x,t) und g(x,t) lösen, wäre u:
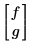
Um die partielle Differentialnotation für tiefgestellte Indizes zu berücksichtigen, können Sie bei Benennungsfunktionen keine tiefgestellten Buchstabenindizes verwenden.
• x ist der Name der räumlichen Variablen.
• xrange ist ein Spaltenvektor mit zwei Elementen, der die reellen Randwerte für x enthält.
• t ist der Name der Zeitvariablen.
• trange ist ein Spaltenvektor mit zwei Elementen, der die reellen Randwerte für t enthält.
• xpts (optional) ist die Ganzzahl der räumlichen Diskretisierungspunkte.
• tpts (optional) ist die Ganzzahl der zeitlichen Diskretisierungspunkte.
Es gelten die allgemeinen Regeln für das Definieren eines Lösungsblocks. Innerhalb des Blockkörpers:
Unbekannte Funktionen
Funktionen müssen anhand ihrer Variablen definiert werden. Verwenden Sie z.B. u(x,t) und nicht u. Um eine partielle Ableitung innerhalb des Lösungsblocks anzugeben, verwenden Sie eine der folgenden Optionen:
• Tiefgestellte Schreibweise. Zum Beispiel ist uxx(x,t) die zweite partielle Ableitung von u nach x.
Tiefgestellte Schreibweise kann nur in pdesolve Lösungsblöcken und nicht in anderen Bereichen des Arbeitsblatts verwendet werden. |
PDE-Gleichungen
Gleichungen müssen mit booleschem Gleichheitszeichen definiert werden. Zweite partielle Ableitungen sind auf der linken Seite von Gleichungen nicht zulässig. Sie müssen Ihre Gleichung in ein Gleichungssystem mit nur ersten Ableitungen umwandeln.
Randbedingungen
Für jede unbekannte Funktion muss es eine Anfangsbedingung u(x,0) und n Randbedingungen geben, wobei n die Ordnung der PDE ist. Randbedingungen können vom Typ Dirichlet (u(0,t) = f(t)) oder Neumann (ux(0,t)=g(t)) sein und an jedem Endpunkt des räumlichen Integrationsbereichs angegeben werden. Die in Randbedingungen verwendeten Endpunkte müssen mit den Endpunkten übereinstimmen, die im Befehl ode/pdesolve angegeben sind. Mathcad überprüft den richtigen Typ und die richtige Anzahl von Randbedingungen und kennzeichnet Fehler mit einer Fehlermeldung.
Randbedingungen
Algebraische Randbedingungen der Form u(x,t)+v(x,t)+w(x,t)=0 sind zulässig. Dadurch wird dem System eine zusätzliche unbekannte Funktion w hinzugefügt, die als eine der Ausgabefunktionen im ode/pdesolve-Aufruf angegeben werden muss. Ungleichheitsbedingungen sind nicht zulässig.
• Weisen Sie die Ausgabe der Funktion pdesolve einem Funktionsnamen oder einem Vektor von Funktionsnamen zu.
• Um die Näherungsmethode für die partiellen Ableitungen zu ändern, klicken Sie mit der rechten Maustaste auf die Funktion pdesolve, und wählen Sie eine andere Methode. Dies kann sich auf die Berechnungszeit auswirken.
• Die numerische Linienmethode eignet sich nur zum Lösen von hyperbolischen und parabolischen PDEs sowie partiellen algebraischen Gleichungen. Verwenden Sie zum Lösen einer Gleichung in einer Programmschleife numol. Verwenden Sie zum Lösen einer elliptischen PDE, z.B. der Poisson-Gleichung, die Funktionen Relax oder Multigrid.
Im Folgenden finden Sie eine Liste möglicher Fehler und Lösungen beim Arbeiten mit pdesolve.
• Fehler: Diese Funktion erfordert mindestens 5 Argumente, wird aber auf 4 angewendet.
Beispiel:
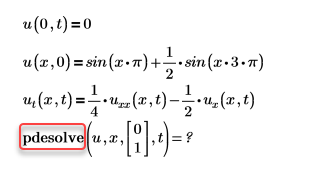
Lösung: Fügen Sie ein fehlendes Argument hinzu, in diesem Fall trange
• Fehler: Diese Funktion akzeptiert höchstens 7 Argumente, ist aber 8 Argumenten zugewiesen.
Beispiel:
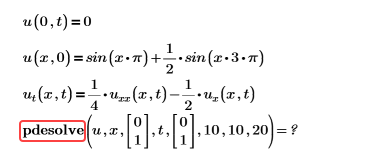
Lösung: Entfernen Sie nicht benötigte Argumente. Weitere Informationen finden Sie in Argumente
• Fehler: Falsch formatierter Vektor der Ränder für Zeitvariable.
Beispiel:
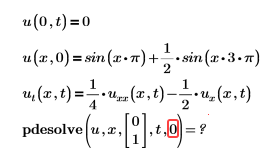
Lösung: trange ist nicht richtig definiert. Weitere Informationen finden Sie in Argumente
• Fehler: Falsch formatierter Vektor der Ränder für Raumvariable.
Beispiel:
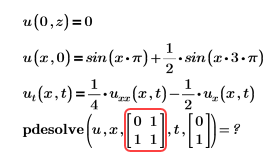
Lösung: xrange ist nicht richtig definiert. Weitere Informationen finden Sie in Argumente
• Fehler: Unbekannte Funktionsnamen falsch angegeben.
Beispiel:
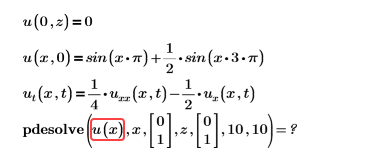
Lösung: Die Funktion muss ohne Argument angezeigt werden.
• Fehler: muss eine Ganzzahl größer als 4 sein.
Beispiel:
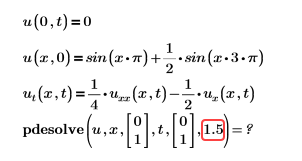
Oder
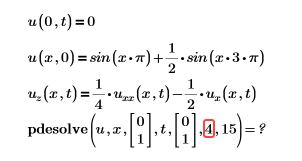
Lösung: Die Anzahl der Diskretisierungspunkte muss eine Ganzzahl größer als 4 sein.