Operatoren für Ableitungen und gewöhnliche Ableitungen
|
Operator
|
Beschreibung
|
Tastaturbefehl
|
|---|---|---|
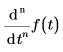 |
Gibt die n-te Ableitung von f(t) in Bezug auf t und am Punkt t ausgewertet zurück.
• Bei einer numerischen Auswertung ist n eine natürliche Zahl zwischen 0 und 5 (einschließlich).
• Bei einer symbolischen Auswertung kann n eine beliebige natürliche Zahl sein.
|
STRG+UMSCHALT+D
|
 |
Gibt die n-te partielle Ableitung von f(t) in Bezug auf t und am Punkt t ausgewertet zurück.
• Bei einer numerischen Auswertung ist n eine natürliche Zahl zwischen 0 und 5 (einschließlich).
• Bei einer symbolischen Auswertung kann n eine beliebige natürliche Zahl sein.
|
Strg+D
|
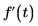 |
Definiert die Funktion g als erste Ableitung der Funktion f(t).
• Sie können n Operatoren "Gewöhnliche Ableitung" schachteln, um die nth Ableitung zu erhalten.
• Für die numerische oder symbolische Auswertung können eine beliebige Anzahl von Operatoren "Gewöhnliche Ableitung" verwendet werden. Die Berechnung der symbolischen Auswertung ist jedoch viel schneller.
|
Strg+ä
|
Operanden
• f(t) ist eine skalarwertige Funktion. Die Funktion kann komplex sein.
◦ Bei Verwendung des Ableitungsoperators kann f(t) eine Funktion mit beliebig vielen Variablen sein.
◦ Bei Verwendung des Operators "Gewöhnliche Ableitung" muss f(t) eine Funktion mit nur einer Variablen sein.
• g ist ein Funktionsname.
• t ist der Punkt, in dem die Ableitung ausgewertet wird.
Zusätzliche Informationen
• Sie können den Exponentenplatzhalter des Ableitungsoperators leer lassen, wenn Sie die erste Ableitung eines Ausdrucks auswerten.
• Die erste Ableitung weist eine Genauigkeit von 7 bis 8 signifikanten Ziffern auf, vorausgesetzt, der Wert, an dem Sie die Ableitung berechnen, liegt nicht zu nahe an einer Singularität der Funktion. Die Genauigkeit sinkt, je höher die Ordnung der Ableitung ist. Dabei gilt im Allgemeinen, dass eine höhere Ordnung der Ableitung mit dem Sinken der Genauigkeit um eine Stelle einhergeht.
• Die numerische Methode zur Berechnung von Ableitungen ist eine Variation der Ridder-Methode, die (n + 1) punktweise dividierte Unterschiede mithilfe zahlreicher Schrittgrößen berechnet, wobei n für die Ordnung der Ableitung steht. Anschließend werden gewichtete Mittelwerte zur Berechnung aufeinanderfolgender Näherungen in einer Tabelle verwendet. Die Einträge der sukzessiven Approximationen werden verglichen und die Approximation mit dem kleinsten Fehler wird als Ableitung zurückgegeben, wenn der Fehler unter einer akzeptablen Größe liegt.