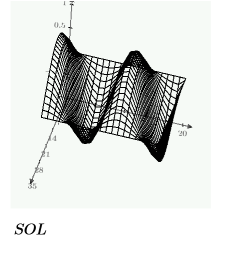
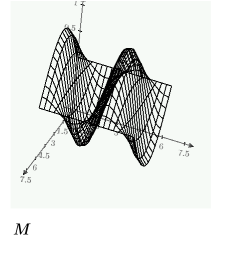
Beispiel: PDE in Lösungsblöcken
Verwenden Sie eine partielle Differentialgleichung (Partial Differential Equation, PDE) im Lösungsblock und den Problemlöser für partielle Differentialgleichungen numol, um Lösungen für eine Wellengleichung zu vergleichen.
Lösungsblock für PDE
So lösen Sie die folgende eindimensionale Wellengleichung:
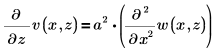
Verwenden Sie die Randbedingung:
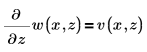
Um die erste Gleichung als System aus zwei partiellen Differentialgleichungen zu definieren, richten Sie einen Lösungsblock für PDE ein.
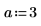
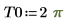
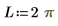
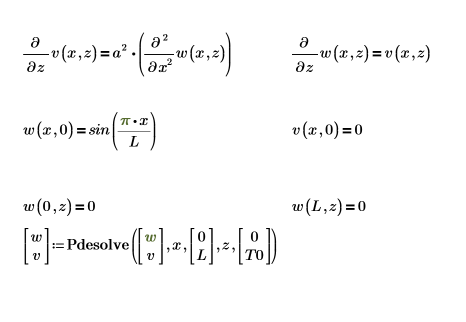
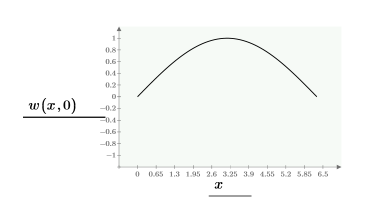
Hier ist eine einzelne Lösung an der Berandung:
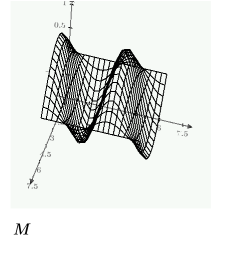
Erstellen Sie ein Raster mit Lösungen, das mit der Funktion CreateMesh dreidimensional geplottet werden soll, und verwenden Sie dabei die oben definierten Randbedingungen:
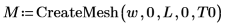
Numol verwenden
Sie können den Befehlszeilen-Lösungsalgorithmus numol lösen. Dies ist besonders hilfreich, wenn Sie die Berechnung in ein Programm einschließen möchten.
Definieren Sie die Anzahl partieller Differentialgleichungen und algebraischer Randbedingungen in Ihrem System:
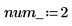
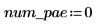
Die Funktion zur Auswertung der rechten Seite der partiellen Differentialgleichungen ist ein Vektor der Länge num_pde + num_pae (partielle algebraische Gleichungen). In diesem Fall ist die Funktion ein Gleichungssystem. Entsprechend wird die Randbedingung als ein Spaltenvektor mit der Länge num_pde + num_pae definiert.
Ausdruck für den Vektor von PDEs:
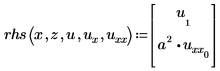
Daher u1=v wie oben definiert und u0=w.
Der Vektor der Anfangsbedingungen:
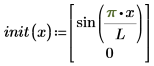
Angenommen, jede linke Seite ist die Zeit-Ableitung erster Ordnung des unbekannten Funktionsvektors u. Die Variablen der Funktion sind x (Raum) und t (Zeit). Die Lösung ist u, die auch ein Vektor von Lösungen für ein Gleichungssystem sein kann: ux, die erste Ableitung jeder Lösung u im Vektor und uxx, die zweite räumliche Ableitung.
Sie müssen tiefgestellte Vektorindizes verwenden, um die einzelnen Einträge in u, ux und uxx anzusprechen.
Der Vektor von Randbedingungen kann über drei Zeilentypen verfügen. Jede Zeile wird durch eine der folgenden Optionen bestimmt:
• rhs enthält räumliche Ableitungen zweiter Ordnung: zwei Randbedingungen (entweder Dirichlet "D" oder Neumann "N") sind erforderlich, eine für jede Seite des Integrationsbereichs.
• rhs enthält räumliche Ableitungen erster Ordnung: eine Dirichlet-Randbedingung auf der linken oder rechten Seite des Integrationsbereichs, die andere ist "NA".
• Wenn der Vektor keine räumlichen Ableitungen enthält, sind keine Randbedingungen erforderlich.
Randbedingungen am linken und rechten Rand folgen den folgenden Konventionen:
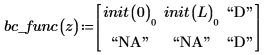
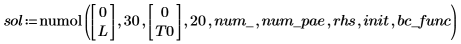
Das Ergebnis von numol ist eine Matrix, die jeden Punkt im Raum als Zeile und jeden Zeitpunkt als Spalte darstellt. Dies erleichtert die Visualisierung von Lösungen, indem Sie eine Spalte nach der anderen auswählen können, um die Lösung zu einem bestimmten Zeitpunkt über den gesamten Raum hinweg darzustellen. Beim Lösen eines Gleichungssystems wird die Lösungsmatrix für jede unbekannte Funktion an die Seite der vorherigen Matrix angehängt.
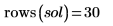
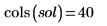
Im aktuellen Beispiel gibt es 20 Zeitpunkte für jede Funktion, sodass die Matrix 40 Spalten enthält. Wählen Sie die erste Lösung, u0:
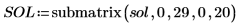
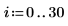
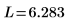
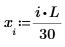
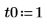
Numol und Pdesolve vergleichen
Vergleichen Sie die Lösungen numol und Pdesolve an einem Punkt t0:
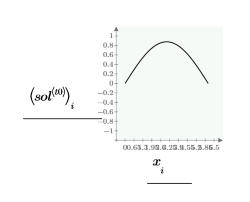
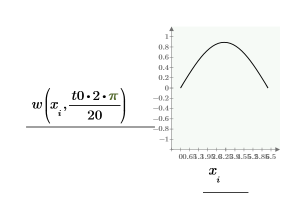
Vergleichen Sie das Raster von Lösungen für die Werte von Raum und Zeit: