Beispiel: Die Hilbert-Transformation
Verwenden Sie die Funktion hilbert, um die Hilbert-Transformation eines reellen Signals zu erstellen, sodass die diskrete Fourier-Transformation des analytischen Signals bei negativen Frequenzen einen Betrag von null aufweist.
1. Verwenden Sie die Funktionen sin und cos, um das Eingangssignal zu definieren. Verwenden Sie die Funktion rnd, um Zufallsrauschen hinzuzufügen.
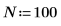
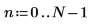
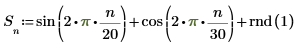
2. Plotten Sie das Eingangssignal.
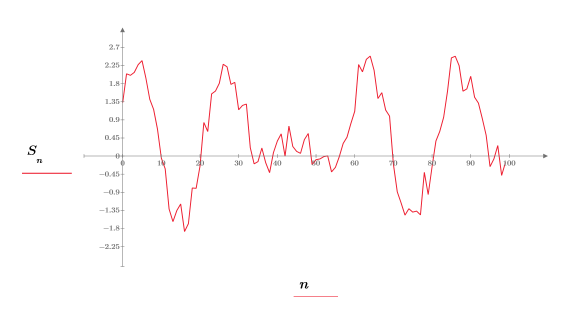
3. Verwenden Sie die Funktion hilbert, um die Hilbert-Transformation des Eingangssignals zu berechnen.
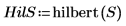
4. Plotten Sie das Hilbert-Transformationssignal.
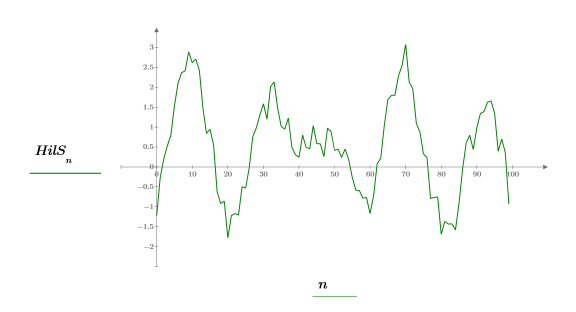
5. Erstellen und plotten Sie das komplexe Signal.
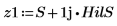
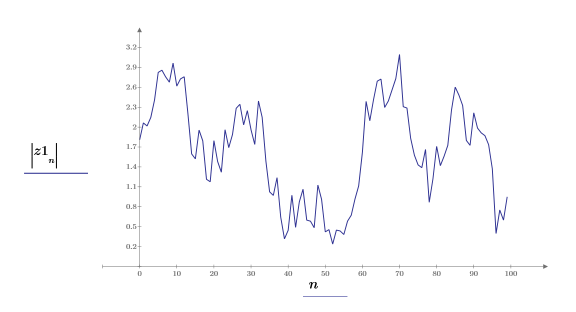
Die nächsten Schritte zeigen, dass der Betrag des analytischen Signals die komplexe Hülle des ursprünglichen Signals darstellt.
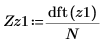
7. Plotten Sie die absoluten Werte des Spektrums.
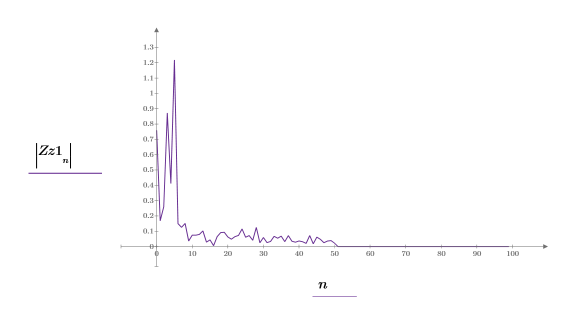
Für Vektoren lautet der Skalierungsfaktor zwischen der Funktion dft und der veralteten Funktion CFFT 1/N.
8. Plotten Sie alle vier Signale in demselben Diagramm.
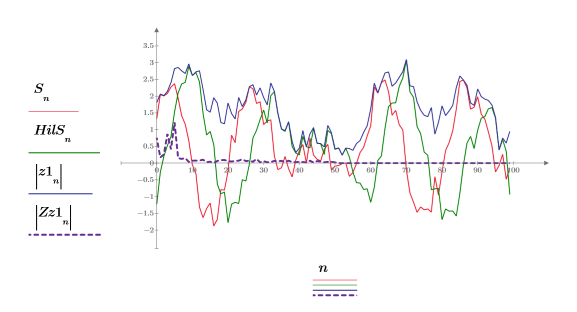
Das neue Signal, das von der Hilbert-Transformation erzeugt wird, steht in folgender Beziehung zum Eingangssignal im Transformationsbereich:
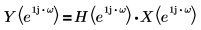
Dabei gilt: H ist der sogenannte Hilbert-Transformator, ein Filter mit folgendem Frequenzgang:
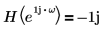 | für | 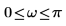 | |
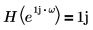 | für | 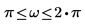 |
Es ist möglich, H mithilfe der Verfahren und Funktionen der Filterkonstruktion zu erstellen.
Idealer Hilbert-Transformator
Rabiner und Gold (Theory and Application of Digital Signal Processing, Prentice-Hall, Inc.) geben Koeffizienten für einen idealen Hilbert-Transformator an. Die Beispiele unten beruhen auf den Erläuterungen in Abschnitt 14.4 im Buch Signal Processing Algorithms von Stearns und David (Prentice-Hall). Die Koeffizienten des idealen Filters werden in einem Fenster dargestellt und verschoben, um einen kausalen Filter ungerader Länge L zu erhalten.
1. Definieren Sie Länge und Mitte.
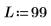
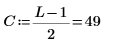
2. Definieren Sie die unbewerteten Koeffizienten h.
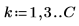 | ||
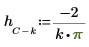 | 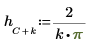 | 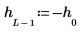 |
3. Verwenden Sie die Funktion hamming, um die Koeffizienten mit einem Hamming-Fenster darzustellen, und multiplizieren Sie dabei mithilfe des vectorize Operators h und das Fenster Element für Element.
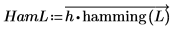
4. Verwenden Sie die Funktion gain, um die Zunahme des Filters bei der Frequenz f mit Koeffizienten h zu berechnen.
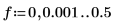
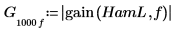
5. Plotten Sie die Zunahme bezogen auf die Frequenz.
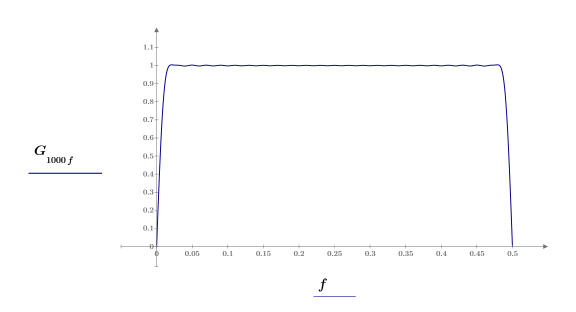
Die Frequenz wird auf eine Abtastfrequenz von 1 normalisiert.
Der Filter hat eine Verzögerung von C, und wir berechnen die Phasenverschiebung des Filters relativ zum verzögerten Signal. Die Verzögerung hat die folgende Übertragungsfunktion:
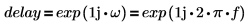 | ||
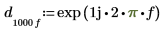 | ||
Dabei gilt: | 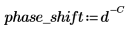 | |
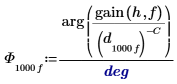 | ||
7. Stellen Sie die Phasenverschiebung in Grad dar.
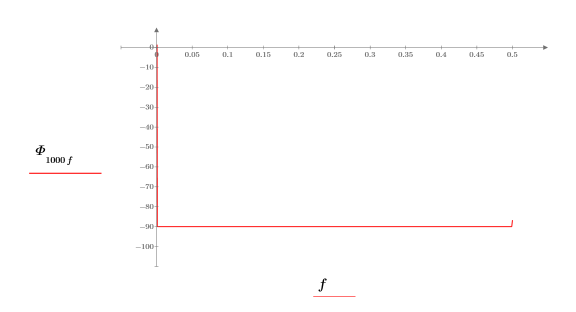
Über nahezu den gesamten Frequenzbereich beträgt die Verschiebung -90 Grad.
Testen des Filters
1. Definieren Sie die Signalparameter.
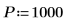
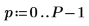
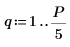
2. Verwenden Sie die Funktion exp, um ein neues Signal zu erstellen. Die Funktion rnd fügt Niederfrequenzrauschen hinzu.
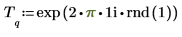
Sie können den Cursor auf rnd setzen und F5 drücken, um eine Neuberechnung durchzuführen und ein anderes Zufallssignal T zu erhalten.
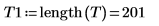
3. Setzen Sie die konjugierten Zahlen dieser Elemente an die letzten 200 Stellen des Signals, um ein reales Ergebnis zu garantieren, wenn es umgekehrt wird.
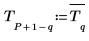
Der neue Vektor hat 1001 Elemente, von denen Elemente 1 bis 200 den ursprünglichen Vektor T und Elemente 801 bis 1000 die konjugierten Zahlen von T enthalten. Dazwischenliegende Elemente werden auf 0 festgelegt.
4. Ermitteln Sie die Fourier-Transformation des Signals T.
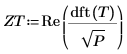
Verwenden Sie die Funktion Re, um den kleinen imaginären Rundungsfehler zu entfernen. Das Rauschen wird durch Erstellen der Transformation T erzeugt, wobei für die ersten 200 Elemente nach dem ersten Element Zufallsphasen und Betragseinheiten verwendet werden.
5. Plotten Sie das transformierte Signal.
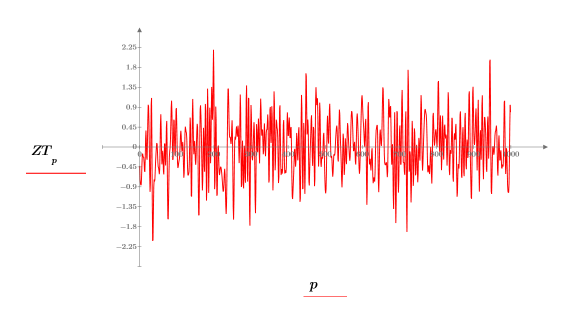
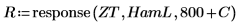
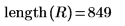
7. Erstellen Sie ein komplexes Signal z2 mit den ersten 800 Elementen von ZT und den letzten 800 Elementen von R.
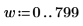
Speichern Sie die ersten 800 Elemente des Fourier-Transformationsvektors ZT in Vektor a2.
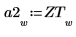
Speichern Sie die letzten 800 Elemente des Ansprechvektors R in Vektor b2.
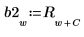
Definieren Sie das komplexe Signal z2.
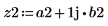
8. Verwenden Sie die Funktion dft, um die diskrete Fourier-Transformation des Signals z2 zu berechnen.
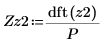
Für Vektoren lautet der Skalierungsfaktor zwischen der Funktion dft und der veralteten Funktion CFFT 1/P.
9. Plotten Sie die absoluten Werte der diskreten Fourier-Transformation des Signals z2.
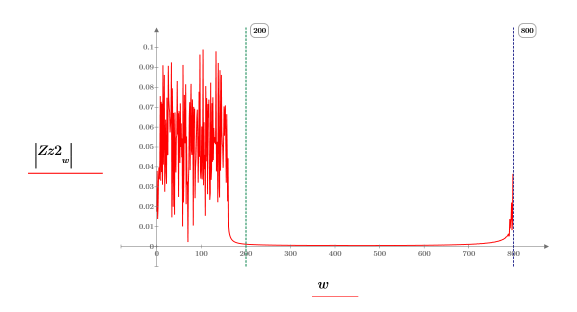
Die ursprünglichen 200 Punkte, die zur Erzeugung des Signals im Transformationsbereich verwendet wurden, sind hier dargestellt. Die obere Hälfte des Spektrums hat im Wesentlichen den Wert null, d.h., der Hilbert-Transformatorfilter hat seine Aufgabe erfüllt.