Beispiel: Wahrscheinlichkeitsverteilungen
Verwenden Sie statt Tabellen Funktionen für die Wahrscheinlichkeitsverteilung.
Wahrscheinlichkeitsdichte
1. Verwenden Sie die Funktion dchisq, um die Wahrscheinlichkeitsdichte einer Chi-Quadrat-Variable mit 11 Freiheitsgraden bei 5.5 zu berechnen:
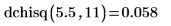
2. Verwenden Sie die Funktion dt, um die Wahrscheinlichkeitsdichte der Variablen t mit vier Freiheitsgraden bei -1.56 zu berechnen:
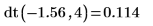
Kumulative Wahrscheinlichkeit
1. Verwenden Sie die Funktion pnorm, um die Wahrscheinlichkeit zu berechnen, dass eine standardnormale Variable 1.0 überschreitet:
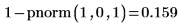
2. Berechnen Sie mit der Funktion pchisq die Wahrscheinlichkeit, dass eine Chi-Quadrat-Variable mit sieben Freiheitsgraden kleiner als 5.6 ist:
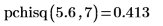
3. Berechnen Sie mit der Funktion pbinom die Wahrscheinlichkeit, dass eine binomische Variable mit der Größe 15 und dem Parameter 0.6 kleiner gleich 10 ist.
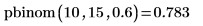
4. Berechnen Sie mit der Funktion qbinom die Wahrscheinlichkeit, dass eine binomische Variable mit der Größe 15 und dem Parameter 0.6 kleiner gleich 10 ist.
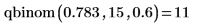
5. Verwenden Sie die Funktion rbinom, um einen Vektor von m=5 Zufallszahlen zu erstellen, die die Binomialverteilung mit der Größe n=7 und der Erfolgswahrscheinlichkeit q=0.65 aufweisen.
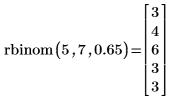
Die Neuberechnung des Arbeitsblatts bewirkt, dass die Funktion rbinom einen neuen Satz von Zufallszahlen zurückgibt. |
6. Berechnen Sie mit der Funktion dbeta die Wahrscheinlichkeitsdichte für den Wert x=0.8 für die reellen Formparameter 3 und 2:
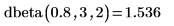
7. Berechnen Sie mit der Funktion pbeta die Wahrscheinlichkeit, dass eine Betavariable mit a=3 und b=2 0.8 überschreitet:
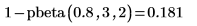
8. Verwenden Sie die Funktion qbeta, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p=0.8 zu berechnen:
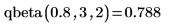
9. Verwenden Sie die Funktion rbeta, um einen Vektor von m=5 Zufallszahlen zu erstellen, die die Binomialverteilung mit der Größe n=6 und der Erfolgswahrscheinlichkeit q=0.75 aufweisen.
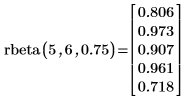
Inverse kumulative Wahrscheinlichkeit
1. Verwenden Sie die Funktion qnorm, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p zu berechnen:
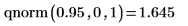
2. Verwenden Sie die Funktion qt, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p zu berechnen:
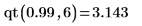
F-Verteilung
1. Berechnen Sie mit der Funktion dF das 65. Perzentil für die F-Verteilung mit vier und sechs Freiheitsgraden:
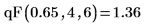
2. Berechnen Sie mit der Funktion pF die kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit 0.75 mit fünf und sieben Freiheitsgraden:
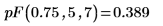
3. Berechnen Sie mit der Funktion qF das 95. Perzentil für die F-Verteilung mit neun und acht Freiheitsgraden:
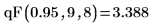
4. Erstellen Sie mit der Funktion rF einen Vektor von sieben Zufallszahlen, die die F-Verteilung mit zwei und drei Freiheitsgraden aufweisen:

Die Neuberechnung des Arbeitsblatts bewirkt, dass die Funktion rF einen neuen Satz von Zufallszahlen zurückgibt. |