Beispiel: Rauschgeneratoren
Verwenden Sie die Funktionen whiten, gaussn und onefn zur Simulation von weißem, Gaußschem bzw. 1/f-Rauschen.
Weißes Rauschen
Die Funktion whiten simuliert das Rauschen, das von N unabhängigen Quellen produziert wird, die jeweils eine zufällige Ausgabe mit einer gleichmäßigen Verteilung zwischen -0.5 und 0.5 erzeugen.
1. Verwenden Sie die Funktion whiten, um die Funktion für weißes Rauschen für sechs unabhängige Rauschquellen auszuwerten.

Die wiederholte Auswertung der Funktion whiten ergibt einen anderen Satz von Vektorelementen.
2. Betrachten Sie einen etwas größeren Ausgabevektor.
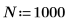
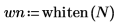
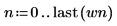
3. Plotten Sie die Funktion für weißes Rauschen.
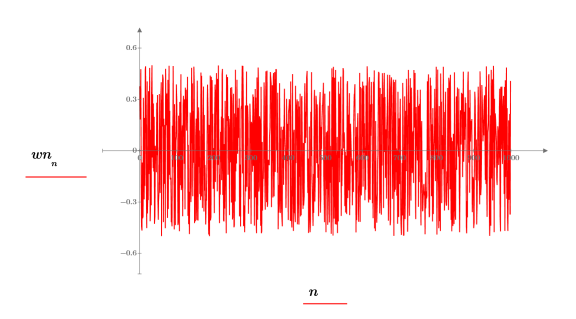
4. Verwenden Sie die Funktionen mean und stdev, um den Mittelwert und die Standardabweichung des Vektors für weißes Rauschen zu berechnen.
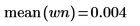
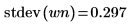
5. Zeigen Sie den theoretischen Wert des Mittelwerts an, und verwenden Sie dann die Funktion var, um die Standardabweichung zu berechnen.
Das Diagramm zeigt, dass das Signal wn einen theoretischen Mittelwert von 0 hat. | |
Die Standardabweichung ist die Quadratwurzel der Varianz. | 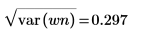 |
6. Vergleichen Sie die berechneten Werte für Mittelwert und Standardabweichung mit den entsprechenden theoretischen Werten, und verifizieren Sie, dass sie nicht wesentlich voneinander abweichen.
Gaußsches Rauschen
Die Funktion gaussn simuliert x unabhängige Rauschquellen, die jeweils eine gaußsche Wahrscheinlichkeitsverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1 aufweisen.
1. Werten Sie die Funktion für das gaussian Rauschen für sechs unabhängige Rauschquellen aus.

Theoretisch können die Elemente des Vektors jeden reellen Wert enthalten, wahrscheinlich liegt ihr Wert jedoch zwischen -3 und +3. Sie können dies überprüfen, indem Sie F5 drücken, um die Funktion neu zu berechnen.
2. Stellen Sie eine gaußsche Beispielsequenz grafisch dar.
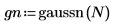
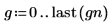
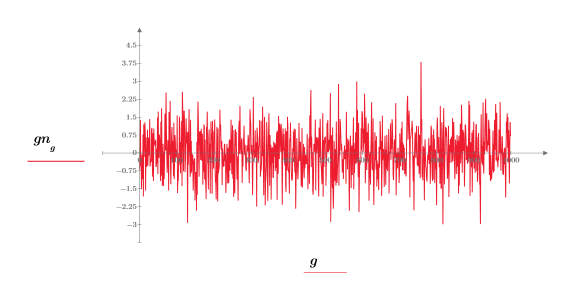
3. Bereiten Sie die gaußschen Daten für eine glockenförmige Histogrammdarstellung vor, indem Sie die Werte in 20 Klassen gruppieren, deren Breite 0.05 beträgt.
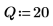
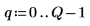
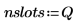
4. Legen Sie den Vektor fest, der die Kanten der Klassen angibt, und geben Sie dann die Berandung ganz rechts an.
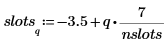
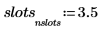
5. Verwenden Sie die Funktion hist, um das Histogramm zu erstellen, und plotten Sie es dann als Säulendiagramm.
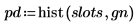
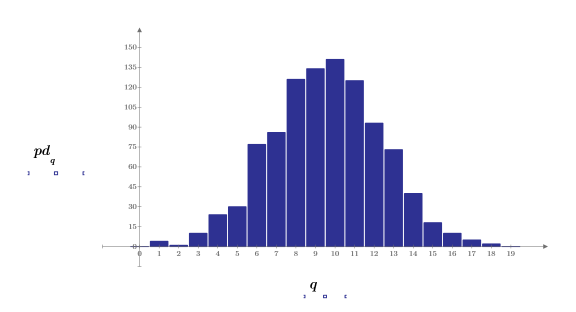
6. Vergleichen Sie Mittelwert und Standardabweichung der Stichprobe mit den erwarteten Werten von 0 und 1.
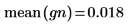
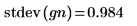
1/f-Rauschen
Die Funktion onefn berechnet mithilfe einer Routine, die auf einem von Richard Voss (siehe Kolumne von Martin Gardner in Scientific American, April 1978) entwickelten Algorithmus basiert, eine Näherung des 1/f-Rauschens.
1. Verwenden Sie die Funktion onefn, um einen 1/f-Vektor mit 1000 Punkten zu generieren.
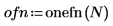
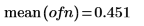
2. Passen Sie sie für den Mittelwert 0 an.
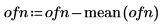
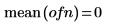
3. Plotten Sie die Vektordaten.
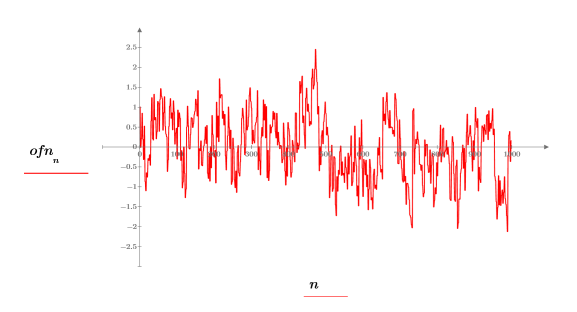
1/f-Rauschen findet sich in den Signalen vieler natürlicher und von Menschenhand geschaffener Phänomene, darunter Musik, Gehirnströme, Wetter, Aktienkursbewegungen und andere hierarchisch interagierende Systeme. Wenn man beispielsweise Musikstücke unterschiedlicher Stilrichtungen (Rock, Jazz, Klassik) digitalisieren würde, würde man feststellen, dass die Verteilung deren spektraler Leistungsdichte der des 1/f-Rauschens sehr nahe kommt.
4. Vergleichen Sie mit der Funktion lcorr die statistische Struktur dieses Rauschens mit dem oben erzeugten weißen Rauschen, indem Sie deren Autokorrelationen berechnen.
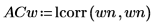
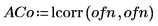
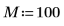
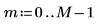
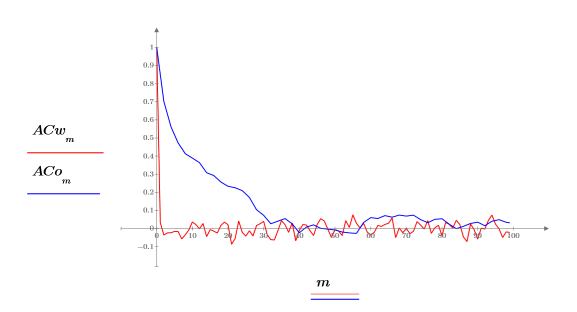
Im Gegensatz zum weißen Rauschen wird das von onefn erzeugte Rauschen korreliert, wobei die Korrelation mit zunehmender Verzögerung abnimmt.
Vergleich von Rauschsignalen mithilfe der spektralen Leistungsdichte
Eine andere Möglichkeit, die Unterschiede zwischen dem weißen Rauschen und dem 1/f-Rauschen zu betrachten, besteht im Vergleich der spektralen Leistungsdichte.
1. Gegeben seien 50 Klassen mit Frequenzgruppen von jeweils 20 Frequenzen.
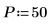
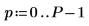
2. Verwenden Sie die Funktionen mag und dft, um die quadrierte Magnitude der Frequenzspektren für jedes Signal zu berechnen.
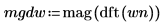
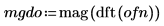
3. Glätten Sie das Ergebnis, indem Sie die Frequenzgruppen mitteln.
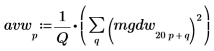
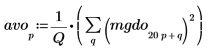
4. Stellen Sie die spektrale Leistungsdichte des weißen Rauschens grafisch dar.
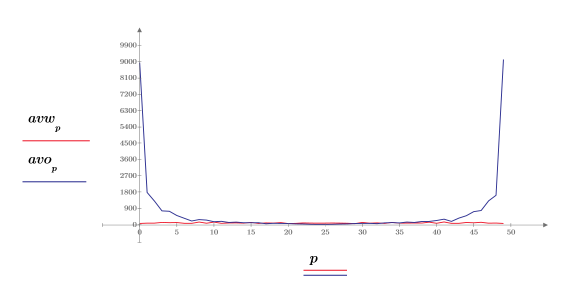
Wie erwartet, ist die spektrale Leistungsdichte des weißen Rauschens im Wesentlichen flach. Das Amplitudenspektrum der 1/f-Näherung fällt mit zunehmender Frequenz stark ab.
5. Verwenden Sie die Funktion log, um den informativeren Logarithmus des Betrages zu berechnen.
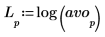
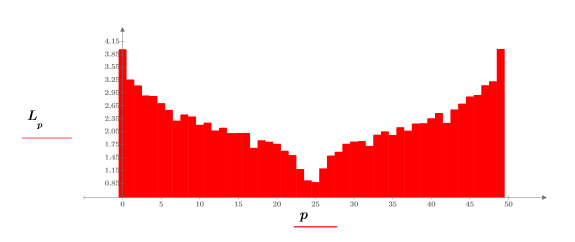
Experiment
Versuchen Sie in diesem Experiment, ein Potenzspektrum von 1/f mit zufällig gewählten Phasen zu konstruieren, und nehmen Sie die inverse Transformation, um den Rauschvektor zu erhalten.
1. Definieren Sie die Breite des Spektrums.
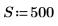
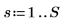
2. Verwenden Sie die Funktion exp, um die erste Hälfte der Transformation zu konstruieren. Ein Potenzspektrum von 1/fentspricht einem Amplitudenspektrum von 1/sqrt(f).
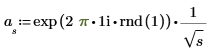
3. Berechnen Sie die zweite Hälfte der Transformation. (Bei einem reellen Signal ist die zweite Hälfte um den Mittelpunkt herum konjugiert-symmetrisch.)
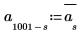
4. Definieren Sie den Mittelwert des Rauschens mit null.
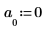
5. Ermitteln Sie mit der Funktion idft die inverse Fourier-Transformation (in den Zeitbereich transformieren).
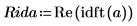
6. Plotten Sie die reellen Werte der inversen Transformation.
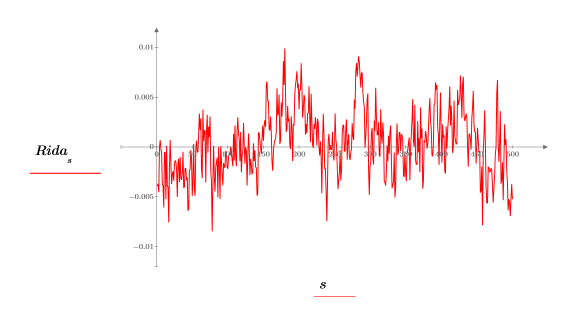
7. Verwenden Sie die Funktion lcorr zur Berechnung der Autokorrelationskurve.
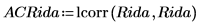
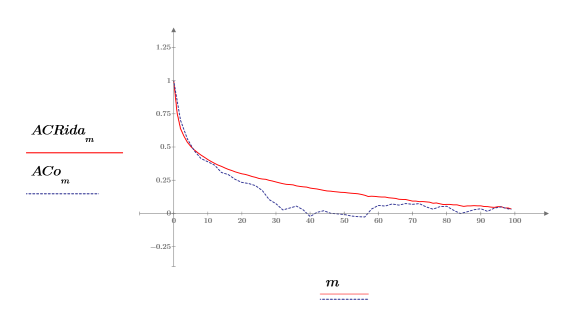
Das Verhalten der Autokorrelation ist der Ausgabe von onefn ähnlich und verfügt über eine Korrelation von 1.0 bei 0 und unterschiedliche Korrelationsgrade an anderen Punkten.