Beispiel: Cholesky-Faktorisierung von komplexen Matrizen

Funktionen > Vektor und Matrix > Matrixfaktorisierung > Beispiel: Cholesky-Faktorisierung von komplexen Matrizen

Verwenden Sie die Funktion Cholesky, um die Cholesky-Faktorisierung einer komplexen Hermitian-Matrix auszuführen.

Um logische Konflikte zu vermeiden, wenn Sie boolesche Vergleiche ausführen, aktivieren Sie Annähernde Gleichheit in der Dropdown-Liste Berechnungsoptionen.

1. Definieren Sie eine komplexe definite quadratische Hermitian-Matrix M.

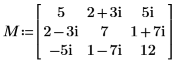
2. Wenden Sie die Funktion eigenvals an, um sicherzustellen, dass die Matrix positiv definit ist.

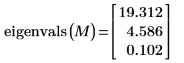
3. Legen Sie die Argumente p und u fest, um das Aktivieren/Deaktivieren der Pivotisierung und der unteren/oberen Faktorisierung zu steuern.

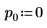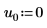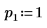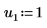4. Verwenden Sie die Funktion Cholesky, um die Standardfaktorisierung der Matrix M durchzuführen - mit Pivotisierung und unterer Faktorisierung.

Die Standardfunktion Cholesky(M) ist mit Cholesky(M,1,0) gleichwertig.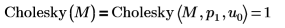

<region id="ID0EJ1KFB" actualWidth="284.50666666666672" actualHeight="27.791200000000003" top="729.60000000000014" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="76">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </math>
</region>

5. Zeigen Sie, dass P10T x M x P10 = L10 x conj(L10T).

<region id="ID0EJ4KFB" actualWidth="165.17000000000002" actualHeight="62.800000000000004" top="825.60000000000014" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="78"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>0</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EX4KFB" actualWidth="371.56" actualHeight="62.800000000000004" top="902.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="80"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L10</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m10</id> <real>1</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>
<region id="ID0EK5KFB" actualWidth="286.33333333333331" actualHeight="62.800000000000004" top="979.20000000000016" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="82"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>	<region id="ID0EY5KFB" actualWidth="273.75666666666666" actualHeight="62.800000000000004" top="1056.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="84"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <conjugate /> <parens> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </parens> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>
<region id="ID0EL6KFB" actualWidth="230.72333333333333" actualHeight="31.752000000000002" top="1113.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="86"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <apply> <mult /> <apply> <transpose /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P10</id> </apply> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id> </apply> <id xml:space="preserve">P10</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L10</id> <apply> <conjugate /> <parens> <apply> <transpose /> <id xml:space="preserve">L10</id> </apply> </parens> </apply> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>

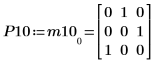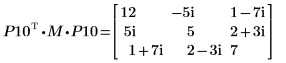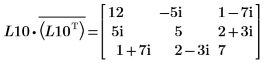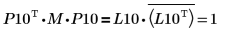Die Beziehung ist logisch wahr.

6. Verwenden Sie die Funktion Cholesky, um die Faktorisierung der Matrix M durchzuführen - mit Pivotisierung und unterer Faktorisierung (Standard).

<region id="ID0EQBLFB" actualWidth="458.07000000000011" actualHeight="62.800000000000004" top="1248.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="88">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m00</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

Die Nichtangabe des Arguments u, wie z.B. in Cholesky(M, 0), entspricht der Einstellung des Arguments auf 0, wie beispielsweise in Cholesky(M, 0, 0).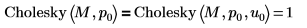

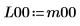
<region id="ID0EJDLFB" actualWidth="307.08666666666676" actualHeight="27.791200000000003" top="1344.0000000000002" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="90">
 <eval xmlns="http://schemas.mathsoft.com/math50">
 <apply>
 <equal />
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id xml:space="preserve">M</id>
 <id xml:space="preserve">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 </sequence>
 </apply>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
 </resultFormat>
 </math>
</region>

Die zurückgegebene untere Matrix L10 bei aktivierter Pivotisierung ist NICHT gleich der zurückgegebenen unteren Matrix L00 bei deaktivierter Pivotisierung.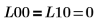

Die Beziehung ist logisch falsch.

7. Zeigen Sie, dass M = L00 x conj(L00T).

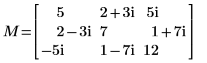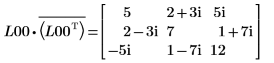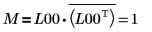Die Beziehung ist logisch wahr.

8. Verwenden Sie die Funktion Cholesky, um die Faktorisierung der Matrix M durchzuführen - mit Pivotisierung und oberer Faktorisierung.

<region id="ID0ENMLFB" actualWidth="452.76666666666671" actualHeight="118.60000000000001" top="1939.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="102">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m11</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

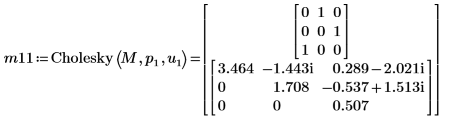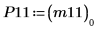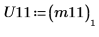9. Zeigen Sie, dass P11T x M x P11 = conj(U11T) x U11.

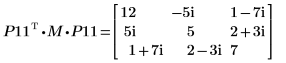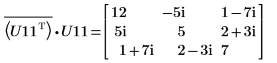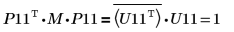Die Beziehung ist logisch wahr.

10. Verwenden Sie die Funktion Cholesky, um die Faktorisierung der Matrix M durchzuführen - ohne Pivotisierung und obere Faktorisierung.

<region id="ID0EWTLFB" actualWidth="478.01333333333338" actualHeight="62.800000000000004" top="2457.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
 <math resultRef="114">
 <define xmlns="http://schemas.mathsoft.com/math50">
 <id labels="VARIABLE" xml:space="preserve">m01</id>
 <eval>
 <apply>
 <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Cholesky</id>
 <sequence>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 p<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">0</Subscript>
 </id>
 <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">
 u<Subscript xmlns="clr-namespace:Ptc.Wpf;assembly=Ptc.Core">1</Subscript>
 </id>
 </sequence>
 </apply>
 <unitOverride>
 <placeholder />
 </unitOverride>
 </eval>
 </define>
 <resultFormat>
 <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" />
 </resultFormat>
 </math>
</region>

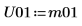
11. Zeigen Sie, dass M = conj(U01T) x U01.

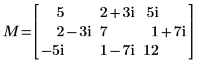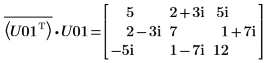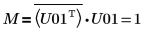Die Beziehung ist logisch wahr.

Zugehörige Themen

Matrixfaktorisierungsfunktionen

War dies hilfreich?