Beispiel: Ermitteln einflussreicher Beobachtungen
Verwenden Sie die Funktion polyfitstat, um die Beobachtungen zu testen, die zum Erzeugen einer multivariaten Polynomregression verwendet wurden.
1. Definieren Sie eine Matrix, die Probenwerte enthält, die bei 20 gesunden Personen zwischen 25 und 34 Jahren gemessen wurden.
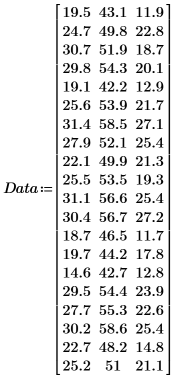
Die Spalten der Matrix stellen die Dicke der Haut am Trizeps, Oberschenkelumfang beziehungsweise Körperfett der 20 Personen dar.
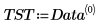
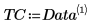
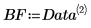
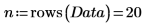
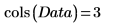
3. Verwenden Sie die Funktion augment, um die Matrix BM als die ersten beiden Spalten der Matrix festzulegen. Verwenden Sie diese Messungen, um den Körperfettanteil der einzelnen Personen vorherzusagen.
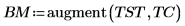
4. Rufen Sie polyfitstat auf, um das Experiment mit einer Regression erster Ordnung zu modellieren und die Regressionsstatistik zu berechnen.
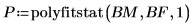
5. Zeigen Sie die Regressionskoeffizientenmatrix an, die Zeile 7 der Ausgabe von P entnommen werden kann.
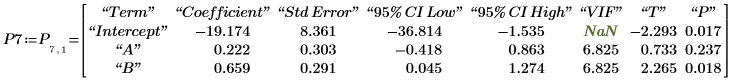
6. Berechnen Sie die Regressionskoeffizienten mit der Matrixberechnung.
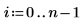
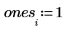
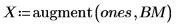
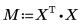
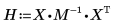
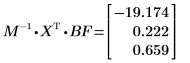
Die Regressionskoeffizienten entsprechen der folgenden Gleichung:
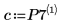
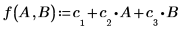
7. Verwenden Sie die Regressionsgleichung, um die vorhergesagte Menge an Körperfett zu berechnen. Vergleichen Sie diese Werte mit dem gemessenen Körperfett.
 |  |
8. Verwenden Sie die Funktion submatrix, um die Modellstatistiken darzustellen, die in den ersten Zeilen der Ausgabematrix P enthalten ist.

Bei der ersten Statistik handelt es sich um die Standardabweichung der Regression.
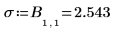
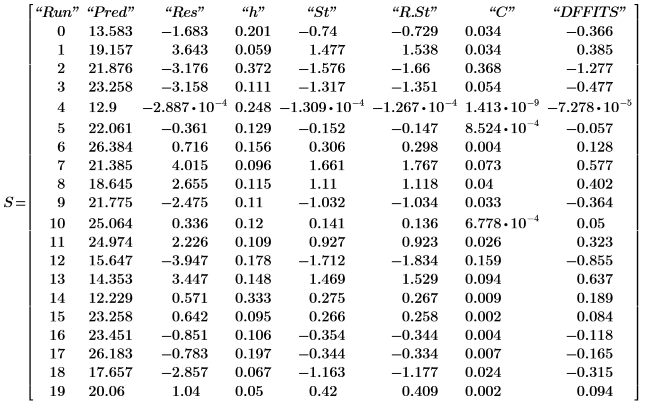
9. Zeigen Sie die Modelldiagnose an, die der letzten verschachtelten Matrix der Ausgabematrix P entnommen werden kann.
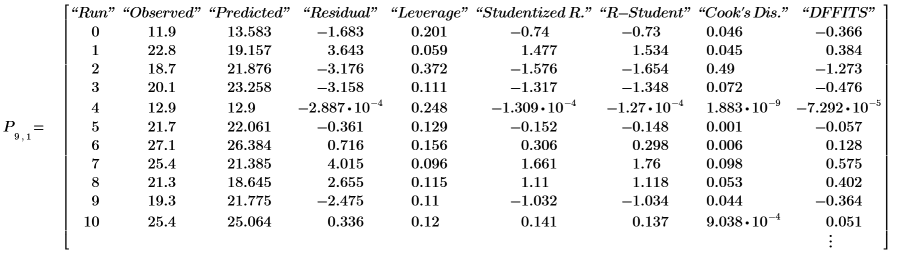
Der beobachtete und der vorhergesagte Wert entsprechen den im 7. Schritt angezeigten Werten. Die Restgrößen sind die Differenz zwischen den beobachteten und den vorhergesagten Werten:
10. Berechnen Sie die Restgrößen bzw. die Differenz zwischen den beobachteten und den vorhergesagten Werten.
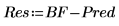
11. Verwenden Sie die Funktion diag, um die Einflusswerte oder die diagonalen Werte der Matrix H zu berechnen.
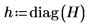
12. Berechnen Sie die Student-verteilten Restgrößen.
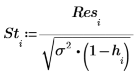
Die externen Student-verteilten Reste (R-Student) werden unten berechnet. Die Konstante p entspricht der Anzahl an Koeffizienten, die für die Regression berechnet wurde, und S2 ist ein Schätzwert für s2, der auf dem Datensatz basiert, aus dem die i-te Beobachtung entfernt wurde.
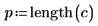
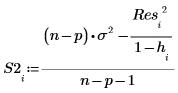
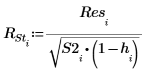
13. Verwenden Sie den Cook-Abstand, um den gesamten Einfluss eines gelöschten Punkts auf eine lineare Regression zu messen.
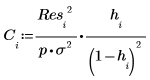
14. Berechnen Sie die Differenz zwischen den vorausgesagten Werten, wenn alle Beobachtungen in die Passform eingeschlossen werden, und den vorausgesagten Werten, wenn die i-te Beobachtung weggelassen wird.
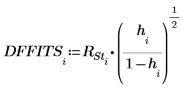
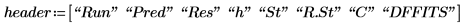
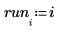
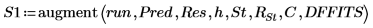
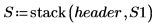
16. Verwenden Sie die Funktionen max und qt, um den größten R-Student-Wert im Datensatz zu ermitteln. Entscheiden Sie mithilfe des Bonferroni-Tests, ob es sich bei der entsprechenden Beobachtung um einen Ausreißer handelt.
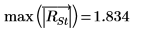
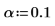
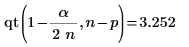
Der größte R-Student-Wert ist kleiner als der Bonferroni-Test, was darauf hinweist, dass es sich bei der entsprechenden Beobachtung um keinen Ausreißer handelt.
17. Ermitteln Sie den maximalen DFFITS-Wert.
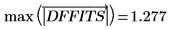
Der Wert ist größer als 1, aber er liegt nah genug an 1, sodass die entsprechende Beobachtung nicht unbedingt einflussreich ist.
18. Erzeugen Sie einen Index Influence-Plot, um die Cook-Abstände für die Durchläufe grafisch darzustellen.
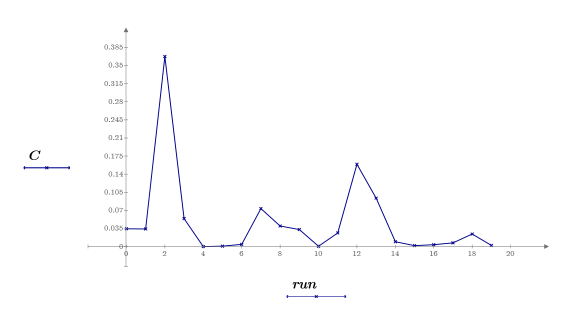
Beobachtung run2 ist die einflussreichste Beobachtung des Datensatzes. Die in Schritt 10 identifizierte Beobachtung für run12 ist auch einflussreich, aber viel weniger als die für run2.
Verweis
Referenz: Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4. Ausgabe, McGraw-Hill/Irwin, Boston, 1996, Seite 375