풀이 구간 정의하기
1. 워크시트에서 풀이 구간을 삽입할 위치를 클릭합니다.
2. Ctrl+7를 누릅니다. 풀이 구간 영역이 나타납니다.
또는 수학 탭의 영역 그룹에서 풀이 구간을 클릭합니다.
3. 선형 방정식 시스템의 경우 풀이 구간 안쪽을 클릭한 다음 각 미지수에 대한 추측값을 정의합니다. 여기에서는 x 및 y를 정의합니다.

4. 부울 연산자를 사용하여 각 미지수에 대한 제약 조건을 정의합니다. Equal To 연산자를 사용하여 두 방정식을 정의합니다.
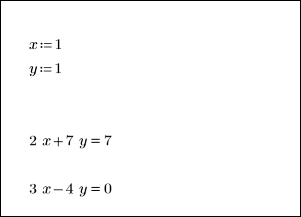
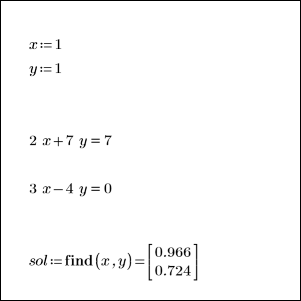
6. 풀이 구간 안에서 부분적으로 정의된 x 및 y가 풀이 구간 밖에서 값이 없는지 확인합니다.
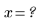
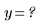
7. 벡터 sol이 정의된 풀이 구간의 오른쪽과 아래쪽에서 값을 가지며 계산에 사용할 수 있는지 확인합니다.
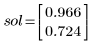
추가 정보
• 선형 또는 비선형 방정식을 풀이하거나 문제를 최적화하는 제약 조건을 정의하려면 다음 연산자를 사용할 수 있습니다.
◦ 부울 Equal To 연산자
◦ 비교 연산자: <, ≤, >, ≥
원하지 않는 중지 점이 발생하지 않도록 비교 연산자를 추가할 수 있습니다.
◦ 추측값 정의에서는 논리 연산자를 사용할 수 있지만 제약 조건 정의에서는 사용할 수 없습니다.
◦ Inequality 연산자 ≠를 사용하여 풀이 구간 내에서 제약 조건을 정의할 수 없습니다.
• 미분 방정식과 관련 초기 또는 경계 조건을 정의하려면 Equal To 연산자를 사용합니다.
• 풀이 구간 내에서 Range 또는 Is Element Of 연산자를 사용하지 마십시오.