예제: 선형 회귀
polyfitc, line, slope 및 intercept 함수를 사용하여 x-y 데이터 집합을 통과하는 최적합 최소자승 선을 찾습니다. stderr 함수를 사용하여 적합식 매개변수의 오차를 계산합니다. 최적합 선을 중심으로 하는 신뢰 한계를 계산하고 신뢰 구간을 정합니다.
최적합 선
다양한 거리를 운전하는 데 걸리는 시간을 추정하는 선형 함수를 만듭니다.
1. 마일 단위의 거리 집합과 해당 거리를 운전하는 데 걸리는 분 단위의 시간을 정의합니다.
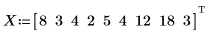
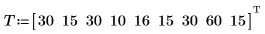
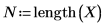
2. 일변수 선형 회귀 방정식을 정의합니다.
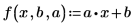
3. polyfitc를 호출하여 회귀 계수 a와 b를 구합니다.
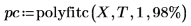
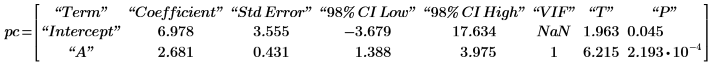
x 값 각각에 대해 T의 값과 회귀 방정식 f를 통해 계산한 값 사이의 차이를 최소화하는 방식으로 계수가 구해집니다. 풀이 구간 및 minimize 함수를 사용하여 제곱의 합을 최소화해 보면 이 사실을 확인할 수 있습니다.

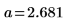
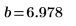
4. 선의 각 점을 기준으로 거리를 측정했을 때 그 거리의 제곱에 대한 합을 최소화하는 최적합 선을 정의합니다.
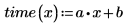
원래 관측한 데이터에 근접한 값에 대해서만 선형 회귀 또는 기타 유형의 회귀를 통해 매개변수화된 방정식을 사용해야 합니다. 위 데이터에 대한 최적합 선을 살펴보면 0마일의 거리를 이동하는 데 다음 시간이 걸린다는 예측이 가능합니다.
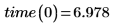
그러나 측정 시간이 엄격한 의미에서 일정한 속도로 이동하는 데 걸리는 시간을 말한다면 이와 같은 예측은 이치에 맞지 않습니다. 이러한 유형의 결과는 때로 특정 물리 현상을 나타낼 수 있습니다. 이 경우 0마일을 운전하는 데 필요한 시간을 신호등 앞에서 기다리는 평균 시간으로 해석할 수 있습니다.
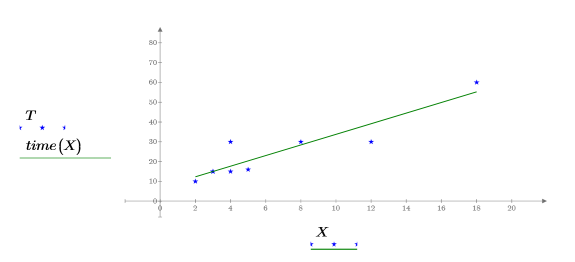
5. 데이터 점과 최적합 선을 도표화합니다.
기울기와 절편을 계산하는 다른 방법
최적합 선의 기울기와 절편을 계산하는 데는 여러 가지 방법이 있습니다. 예를 들어 line 함수를 사용하여 slope 함수와 intercept 함수를 결합할 수 있습니다. 또 다른 방법으로는 행렬 계산이나 통계 관계를 사용하는 방법이 있습니다.
1. intercept 및 slope 함수를 호출합니다.
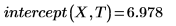
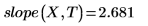
2. line 함수를 호출합니다.
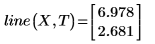
3. augment 함수를 통해 행렬 계산을 사용합니다.
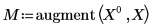
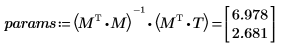
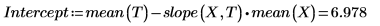
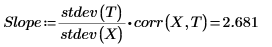
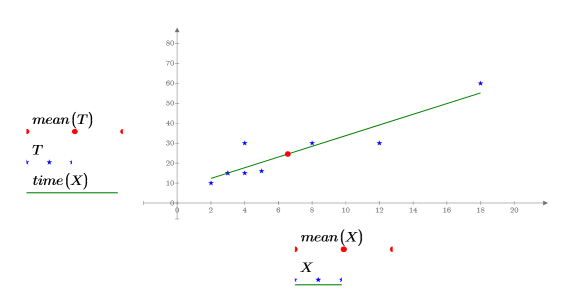
5. 도표를 사용하여 최소자승 선이 항상 (mean(X), mean(T)) 점을 통과한다는 것을 보여줍니다.
표준 오차
추정치의 표준 오차(단순히 표준 오차라고도 함)를 계산하여 위의 선형 적합이 얼마나 정확한지 측정합니다. 기울기와 절편의 오차도 계산합니다.
1. 자유도(데이터 점의 수에서 적합식 매개변수의 수를 뺀 값)를 정의합니다.
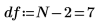
2. stderr 함수를 호출하여 앞서 정의한 최적합 선에 대한 추정치의 표준 오차를 계산합니다.
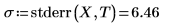
이는 MSE(평균 제곱 오차)의 제곱근, 즉 σ2의 제곱근입니다.
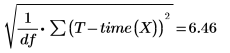
3. 계산된 표준 오차와 polyfitstat 함수로 구한 표준 오차를 비교합니다.
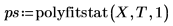
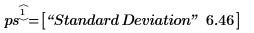
4. 기울기와 절편의 표준 오차를 계산합니다.
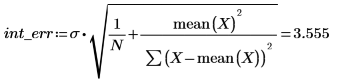
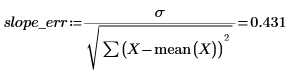
5. 행렬 계산을 사용하여 위 계산을 반복합니다.
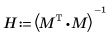
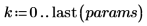
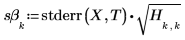
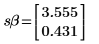
6. augment 함수를 사용하여 각 회귀 계수의 표준 오차가 polyfitc 함수로 구한 행렬에 기록된다는 것을 보여줍니다.
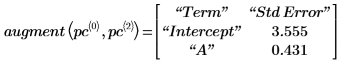
각 계수의 신뢰 구간
위의 추정치를 스튜던트의 t 분포에서 가져온 백분위수 점과 함께 사용하여 기울기와 절편의 추정치에 대한 신뢰 구간을 정합니다.
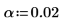
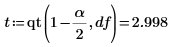
2. 기울기의 신뢰 한계를 계산합니다.
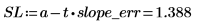
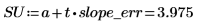
실제 기울기 값이 SL과 SU 사이에 놓일 가능성이 98%입니다.
3. 절편의 신뢰 한계를 계산합니다.
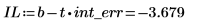
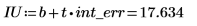
이 값의 범위가 넓다는 것은 데이터가 산점해 있는 정도가 심하다는 의미입니다.
4. confidence 함수를 호출하여 1-3단계를 반복합니다.
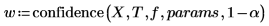
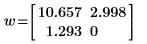
confidence 함수는 첫째 열의 신뢰 구간 너비와 둘째 열의 t 인수를 구합니다. 너비를 t 인수로 나누면 두 매개변수에 표준 오차가 다시 나옵니다.
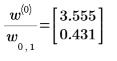
5. 신뢰 한계를 구하려면 관련 매개변수에서 너비를 더하거나 뺍니다.
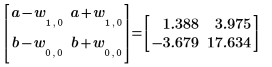
6. augment 함수를 사용하여 각 회귀 계수의 표준 오차가 polyfitc 함수로 구한 행렬에 기록된다는 것을 보여줍니다.

회귀의 신뢰 구간
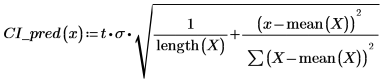
2. 위 함수를 사용하여 임의의 x 예측값에 대한 신뢰 구간을 계산합니다.
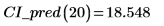
3. 행렬 계산을 사용하면 다음과 같습니다.
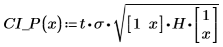
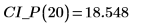
4. 전체 회귀 영역에 대해 데이터, 최적합 선 및 신뢰 구간을 도표화합니다.
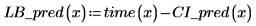
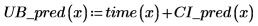
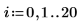
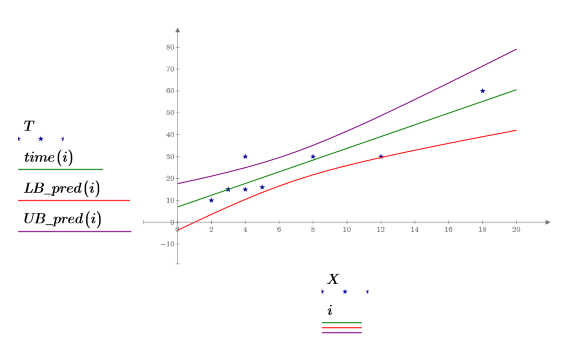
예측값의 신뢰 영역이 측정값 중앙에 가까울수록 잘록하게 들어가는 것을 알 수 있습니다. 회귀를 계산하는 데 사용한 수식이 평균을 기반으로 하므로 데이터의 평균에 근접할수록 예측값이 더 정확해지기 때문입니다.
5. 측정값에 대한 신뢰 한계를 계산합니다. 이 한계는 예측값에 대한 한계와 약간 다릅니다.
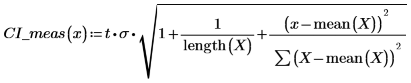
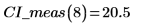
6. 행렬 계산을 사용하면 다음과 같습니다.
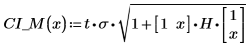
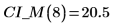
7. 신뢰 한계를 오차 그래프선으로 도표화합니다.
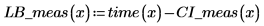
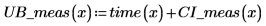
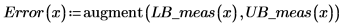
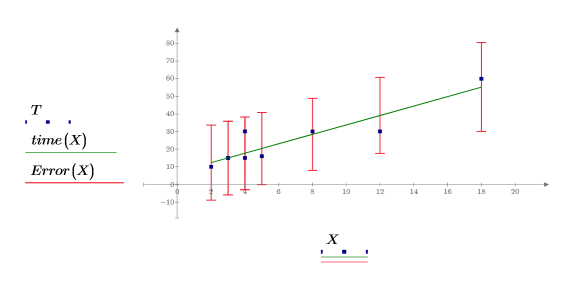
신뢰 구간을 벗어난 측정값이 이상치를 나타내므로 이상치를 검출하는 데 그래프를 사용할 수 있습니다. |