Relaxation Method for a PDE
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
Return a square matrix in which an element's location in the matrix corresponds to its location within a square region, and an element's value approximates the solution to Poisson's Partial Differential Equation (PDE)
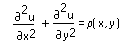
at that point. The relax function solves Poisson's Equation using modified Gauss-Seidel with successive overrelaxation over the grid.
The multigrid function solves for the special case where all boundary conditions in U are zero, using the multigrid method.
• If your boundary conditions are constant and equal on all four sides, transform the equation to have zero boundary conditions on all sides and use multigrid, as it is faster and easier to set up.
• Poisson's equation reduces to Laplace's equation in the case ρ = 0.
• If you are trying to solve a hyperbolic or parabolic PDE, or system of PDEs, use numol.
Arguments
• A, B, C, D, E are real square matrices of the same size containing coefficients of the discretized Laplacian approximation to the function u at the four nearest neighbors and the approximation point.
• S is a square matrix containing the source term at each point inside the square.
• U is a square matrix containing boundary values along the edges of the region and initial guesses for the solution inside the region.
• rjac is a real value 0 < rjac < 1, the spectral radius of the Jacobi iteration. This controls the convergence of the relaxation algorithm.
The optimal value of rjac depends on the details of your problem, but r is a good starting value, where n is the number of points in each direction on the grid:
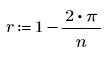
• M is a 1 + 2n square matrix whose elements correspond to the source term at the corresponding point in the square domain.
• ncycle is the integer number of cycles at each level of the multigrid iteration.
An ncycle value of 2 generally gives a good approximation of the solution.