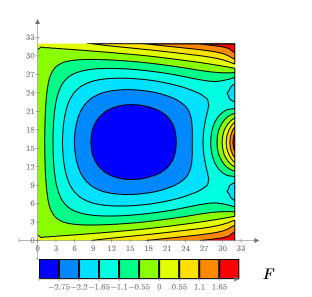
Example: Heat Flow on a Square Plate

Functions > Solving and Optimization > Differential Equation Solvers > Example: Heat Flow on a Square Plate - II

Example: Heat Flow on a Square Plate - II

Solve for the steady-state temperature distribution of a square plate using the partial differential equation solver relax.

Solving Poisson's Equation

Solve the heat equation where values of the source function are known and the boundary conditions are non-zero.

The relax function is based on an entirely different solving method, and hence requires a different set of arguments.

1. Define five square matrices a, b, c, d, and e to contain the coefficients for the Laplacian approximation:

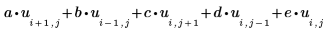
These arrays can be of any size you specify. The larger they are, the finer the mesh in the solution.

2. Define the dimension of the square plate:

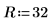
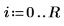
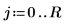
3. Define the coefficients:

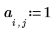
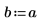
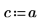
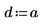
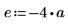
4. Define the strength and position of a constant source.

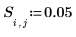
5. Define a square matrix f, of size equal to the size of the grid, to contain the known boundary values of function F(x,y) and guess values for the unknown interior values.

◦ Boundary condition along the top:

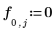
◦ Boundary condition along the bottom:

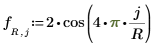
◦ Boundary condition along the edges:

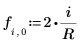
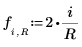
6. Define the Jacobi spectral radius variable r, a real number between 0 and 1.

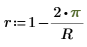
This parameter controls the convergence of the algorithm. If you see the error message "too many iterations", then try reducing r.

7. Call the relax function:

<region id="ID0EJNQ5" top="1516.8000000000002" left="38.400000000000006" height="25.6" width="204.10333333333335" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">F</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">relax</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">a</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">b</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">c</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">d</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">e</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">f</id>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">r</id>
        </sequence>
      </apply>
    </define>
  </math>
</region>

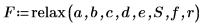
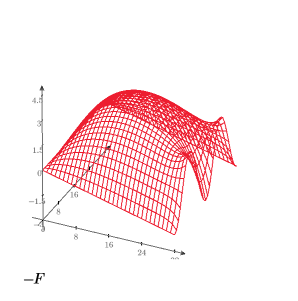
8. Create a 3D plot to show the heat distribution over the square plate.

<region id="ID0EZOQ5" top="1747.2000000000003" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="32" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-3" end="4.5">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">F</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.052623873051966662</Cell>
          <Cell>0.043294250885890617</Cell>
          <Cell>0.99767546618388891</Cell>
          <Cell>0</Cell>
          <Cell>0.095704097834471175</Cell>
          <Cell>0.99467978821191028</Cell>
          <Cell>-0.038116198399097093</Cell>
          <Cell>0</Cell>
          <Cell>-0.99401783366431629</Cell>
          <Cell>0.093475808436936883</Cell>
          <Cell>-0.056487340124674094</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthographic</CameraType>
    </plot3D>
  </plot>
</region>

9. Create a contour plot to show the lines of constant temperature.