Example: Heat Flow on a Square Plate

Functions > Solving and Optimization > Differential Equation Solvers > Example: Heat Flow on a Square Plate - I

Example: Heat Flow on a Square Plate - I

Solve for the steady-state temperature distribution of a square plate using the partial differential equation solver multigrid.

Solving Laplace's Equation

Find the temperature T(x,y) of a square plate with a constant internal heat source. The boundary of the source is pinned at zero degrees.

1. Define the dimension of the square plate:

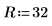
2. Write a Laplace equation, in two variables, to represent points on the plate that are free of the heat source:

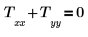
3. Set the dimensions of the heat source ρ:

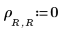
4. Define the position of the heat source:

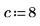
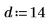
5. Define the strength of the heat source:

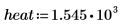
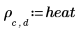
6. Set the number of cycles at each level of multigrid iteration:

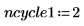
7. Use function multigrid to find the solution:

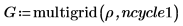
8. Create a 3D plot to show the heat distribution over the square plate:

<region id="ID0EBQO5" top="1036.8000000000002" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="56" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FFED1D2F">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="0" end="1.25">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <apply xmlns="http://schemas.mathsoft.com/math50">
              <neg />
              <id xml:space="preserve">G</id>
            </apply>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>-0.033544651990996412</Cell>
          <Cell>0.15928240904068555</Cell>
          <Cell>0.98666299742769259</Cell>
          <Cell>0</Cell>
          <Cell>0.30398219843693014</Cell>
          <Cell>0.942073234763303</Cell>
          <Cell>-0.14174922707393303</Cell>
          <Cell>0</Cell>
          <Cell>-0.95208695997595394</Cell>
          <Cell>0.29517305858225334</Cell>
          <Cell>-0.080020535682685218</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthographic</CameraType>
    </plot3D>
  </plot>
</region>

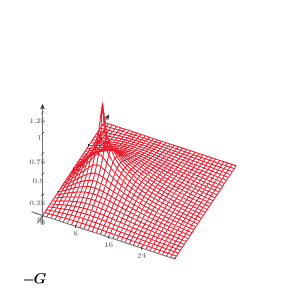
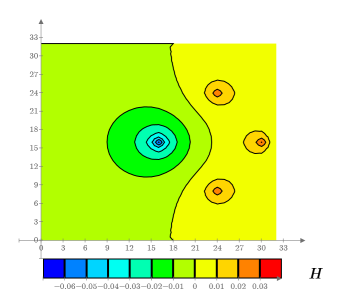
9. Create a contour plot to show the lines of constant temperature:

10. Define a different configuration of heat sources positioned at different locations:

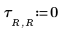
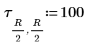
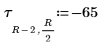
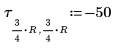
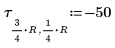
11. Set the number of cycles at each level of the multigrid iteration:

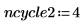
12. Use function multigrid to find the solution:

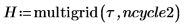
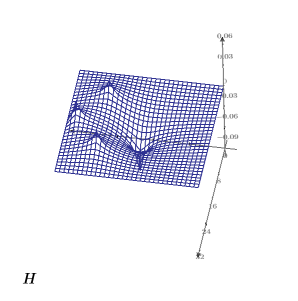
13. Create a 3D plot to show the heat distribution over the square plate:

<region id="ID0ERZO5" top="2265.6000000000004" left="38.400000000000006" height="301.40000715255735" width="297.6000071525574" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white">
    <plot3D>
      <traces>
        <trace3D resultRef="76" num-of-points="41" SurfaceFill="#00FFFFFF">
          <traceStyle color="#FF2E3192">surface</traceStyle>
        </trace3D>
      </traces>
      <graph-size width="240.00000715255737" height="240.00000715255737" />
      <axes>
        <xAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </xAxis>
        <yAxis rank="1" start="0" end="32">
          <axisLine />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <xyDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </xyDomain>
        </yAxis>
        <zAxis rank="1" start="-0.09" end="0.06">
          <axisLine />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <numberFormat>
            <general precision="3" />
          </numberFormat>
          <zDomain auto-scale="true" allow-negative-values="true" scale-type="linear">
            <startValue />
            <endValue />
          </zDomain>
        </zAxis>
      </axes>
      <plotEquations>
        <plotEquation>
          <math>
            <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">H</id>
          </math>
          <math>
            <placeholder xmlns="http://schemas.mathsoft.com/math50" />
          </math>
        </plotEquation>
      </plotEquations>
      <CameraTransformMatrix Columns="4" Rows="4">
        <Cells>
          <Cell>0.28776910670726691</Cell>
          <Cell>0.14277686867570288</Cell>
          <Cell>-0.94699720537922527</Cell>
          <Cell>0</Cell>
          <Cell>-0.33031167875973361</Cell>
          <Cell>0.942946222767463</Cell>
          <Cell>0.04179253334628906</Cell>
          <Cell>0</Cell>
          <Cell>0.89893444482889184</Cell>
          <Cell>0.30077763670149293</Cell>
          <Cell>0.31851165937911374</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>0</Cell>
          <Cell>1</Cell>
        </Cells>
      </CameraTransformMatrix>
      <CameraType>Orthographic</CameraType>
    </plot3D>
  </plot>
</region>

14. Create a contour plot to show the lines of constant temperature: