Sine and Cosine Integrals

Functions > Symbolic Functions > Sine and Cosine Integrals

• Si(x)—The Sine integral function is defined as:

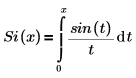
The series expansion representation is:

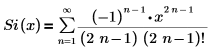
The displayed result represents, three out of the default six, terms of the series that do not have coefficients of 0.

<region id="ID0EIT5BB" actualWidth="187.70000000000002" actualHeight="52.158666666666669" top="192.00000000000003" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="30">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Si</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <minus />
            <id xml:space="preserve" labels="*">x</id>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>3</real>
              </apply>
              <real>18</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>5</real>
            </apply>
            <real>600</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

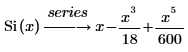
• Ci(x)—The Cosine integral function is defined as:

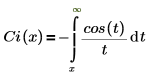
Another form of the definition is:

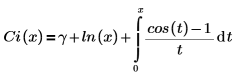
The series expansion representation is:

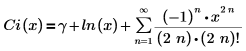
The last two terms represent, two out of the default six, terms of the series that do not have coefficients of 0.

<region id="ID0EVW5BB" actualWidth="234.19000000000003" actualHeight="52.158666666666669" top="460.80000000000007" left="364.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="38">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Ci</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <minus />
            <apply>
              <plus />
              <id xml:space="preserve" labels="CONSTANT">γ</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ln</id>
                <id xml:space="preserve" labels="*">x</id>
              </apply>
            </apply>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>2</real>
              </apply>
              <real>4</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>4</real>
            </apply>
            <real>96</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

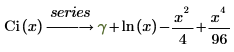
• Shi(x)—The Hyperbolic sine integral function is defined as:

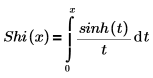
The displayed result represents, three out of the default six, terms of the series that do not have coefficients of 0.

<region id="ID0E3Y5BB" actualWidth="196.13333333333335" actualHeight="52.158666666666669" top="595.2" left="19.200000000000003" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="42">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Shi</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <plus />
            <id xml:space="preserve" labels="*">x</id>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>3</real>
              </apply>
              <real>18</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>5</real>
            </apply>
            <real>600</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

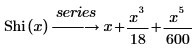
The terms of the series expansion of the Si and Shi functions are identical except for the sign of the terms where n is even.

• Chi(x)—The Hyperbolic cosine integral function is defined as:

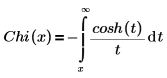
Another form of the definition is:

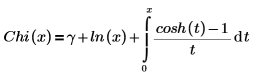
The last two terms represent, two out of the default six, terms of the series that do not have coefficients of 0.

<region id="ID0EH35BB" actualWidth="242.62333333333336" actualHeight="52.158666666666669" top="806.40000000000009" left="364.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="48">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">Chi</id>
        <id xml:space="preserve">x</id>
      </apply>
      <command>
        <id xml:space="preserve">series</id>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <plus />
            <apply>
              <plus />
              <id xml:space="preserve" labels="CONSTANT">γ</id>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ln</id>
                <id xml:space="preserve" labels="*">x</id>
              </apply>
            </apply>
            <apply>
              <div />
              <apply>
                <pow />
                <id xml:space="preserve" labels="*">x</id>
                <real>2</real>
              </apply>
              <real>4</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <pow />
              <id xml:space="preserve" labels="*">x</id>
              <real>4</real>
            </apply>
            <real>96</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

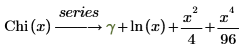
The terms of the series expansion of the Ci and Chi functions are identical except for the sign of the terms where n is odd.

Arguments

• x is a real or complex scalar, or a vector of real or complex scalars.

Additional Information

These functions are useful with using the float keyword that numerically evaluates functions instead of returning symbolic math.