To Expand an Expression into a Taylor or Laurent Series
1. Place the cursor at the end of a function, insert the symbolic evaluation operator, and type the keyword series in the placeholder.
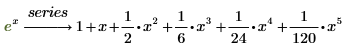
The resulting series contains a large number of terms with non-zero coefficients of odd and even powers of x, but PTC Mathcad returns, by default, the first six terms. Specify keyword series,6 and verify that you get the same result.
• If the first non-zero term of the series corresponds to xn, then PTC Mathcad returns the terms from xn to xn+k-1. • For the above example, n=0, k=6, and n+k-1=5, and the last displayed term contains x5. • PTC Mathcad does not display terms that have coefficients of 0 |
2. To return a different number of terms, type a comma after the keyword, followed by a positive integer k.
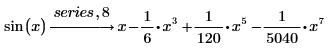
The above evaluation calls for returning the expansion terms of the sin function up to the term that contains xn+k-1 or x7, but the result contains four terms only. This is because the terms that contain x0, x2, x4, x6 have coefficients of 0 and thus are not displayed.
3. To expand an expression around a point other than 0, specify a value for the variable after the keyword series, using the Boolean equal operator.
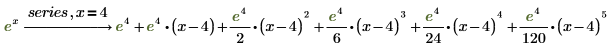
• By default, PTC Mathcad expands the function about point 0. • If the expression contains more than one variable, type a comma after series, and then type a comma-separated list of variables around which you want to expand the series. |