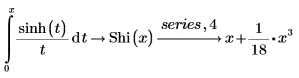Example: Working with Sine and Cosine Integral Symbolic Functions
This example demonstrates the various representations of the sine and cosine integral functions, and of the hyperbolic sine and cosine integral functions.
The Sine and Cosine Integral Functions
1. Type in the series expansion representation of the sine integral function and evaluate it symbolically.
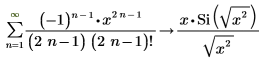
2. Use the simplify and assume keywords to evaluate the same expression.
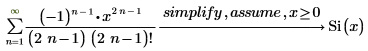
PTC Mathcad Prime evaluates this expression as the Si function.
3. Use the series keyword to get the default first six terms of the series.
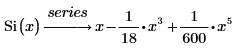
PTC Mathcad Prime does not display terms that have zero coefficients.
4. Find the first 10 terms of the series.
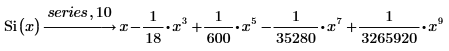
5. Type in, and symbolically evaluate, the series expansion representation of the cosine integral function.
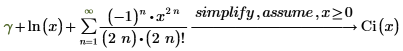
PTC Mathcad Prime evaluates this expression as the Ci function.
The Hyperbolic Sine and Cosine Integral Functions
Explicitly define the hyperbolic sine integral function, symbolically evaluate it, and find the first four terms of the series.