変更因子について
変更因子とは、キーワードの挙動を修正するために使用する特別な用語です。たとえば、変更因子 real をキーワード assume の後に付けて、変数は実数でなければならないことを指定します。
使用可能な変更因子と、対応する有効なキーワードは次のとおりです。
|
変更因子
|
説明
|
キーワードとの使用
|
|---|---|---|
|
ALL
|
式の各変数にキーワードを適用します。
|
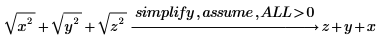 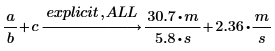 |
|
acos
|
式を逆余弦関数で書き換えます。
|
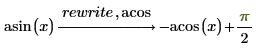 |
|
acot
|
式を逆余接関数で書き換えます。
|
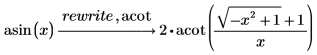 |
|
arg
|
π を含む −π から π までの z の主偏角を返します。z が |z|·e^i·θ として書かれている場合、主偏角は θ の値になります。
|
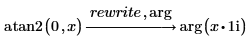 |
|
asin
|
式を逆正弦関数で書き換えます。
|
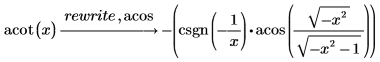 |
|
atan
|
式を逆正接関数で書き換えます。
|
rewrite
combine
|
|
atan2
|
式を逆正接関数で書き換えます。
|
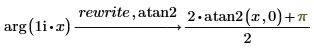 |
|
積分のコーシー主値を返します。
|
整数のシンボリック評価 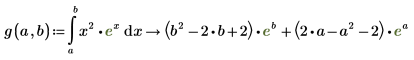 |
|
|
complex
|
変数が複素数であること、つまり演算を複素数に実行することを指定します。
|
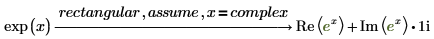 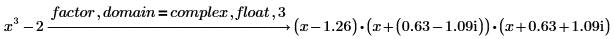 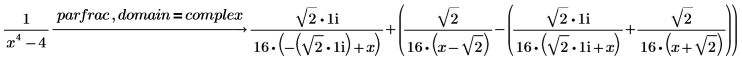 |
|
cos
|
式を余弦関数で書き換えます。
|
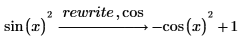 |
|
cosh
|
式を双曲線余弦関数で書き換えます。
|
rewrite
|
|
cot
|
式を余接関数で書き換えます。
|
rewrite
|
|
coth
|
式を双曲線余接関数で書き換えます。
|
rewrite
|
|
項の次数を含む coeffs の出力の 2 列目を返します。
|
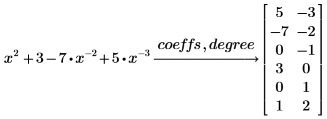 |
|
|
domain
|
キーワード factor の場合
• ドメインが real の場合 - 入力数式の実根で分解
• ドメインが complex の場合 - 入力数式のすべての根で分解
キーワード parfrac の場合
• ドメインが real の場合 - 分母の実根に従って分解
• ドメインが complex の場合 - 分母のすべての根で分解
|
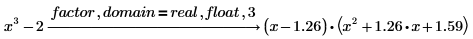 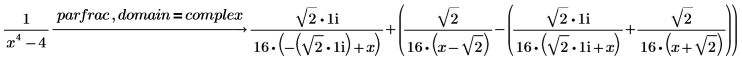 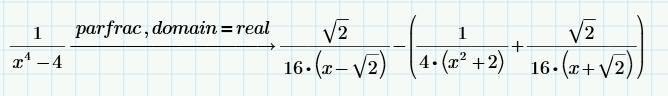 |
|
変数が 2 で割り切れる整数であることを示します。
|
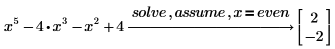 |
|
|
exp
|
指数関数の公式を使用して式を結合または書き換えます。
|
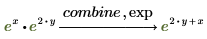 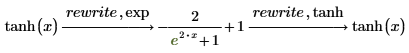 |
|
fact
|
階乗項を含む計算を返します。
|
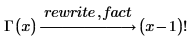 |
|
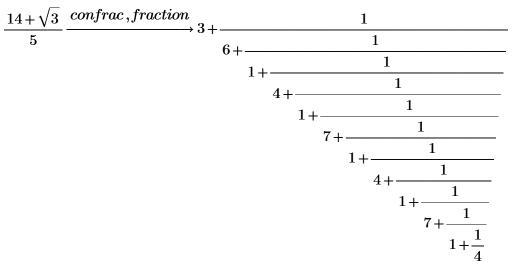
分数として連分数を返します。
|
 |
|
|
方程式の詳細解を返します。
|
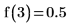 substitute series simplify fourier rewrite rectangular parfrac |
|
|
gamma
|
階乗を含む式を、ガンマ関数を使用して書き換えます。
|
 |
|
解に生成された変数について、キーワード solve とともに使用されるときに、仮説を立てます。結果をドメイン (複素数または実数) あるいは条件 (>、<、=) でフィルタします。
|
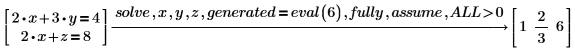 |
|
|
Φ (Heaviside)
|
式を Heaviside 関数で書き換えます。
|
rewrite
|
|
変数は整数であると指定します。
|
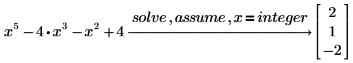 |
|
|
ln
|
自然対数関数の公式を使用して式を結合または書き換えます。
|
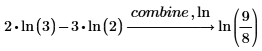 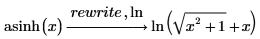 |
|
log
|
常用対数関数の公式を使用して式を結合または書き換えます。
|
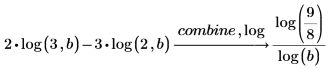 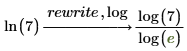 |
|
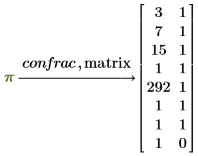
matrix
|
連分数を配列形式で返します。
|
 |
|
max
|
simplify アルゴリズムの追加手順を実行して、式をより簡素化します。
|
fully
simplify
|
|
nfact
|
フーリエ変換の規格化因子を設定します。
|
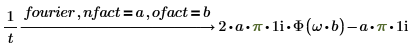 |
|
変数が 2 で割り切れない整数であることを示します。
|
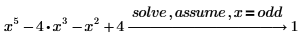 |
|
|
ofact
|
フーリエ変換の振動因子を設定します。
|
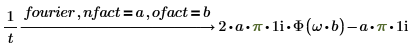 |
|
raw
|
簡素化していない形式で結果を返します。
|
fourier
invfourier
laplace
invlaplace
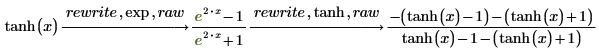 ztrans invztrans 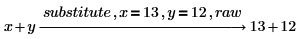 |
|
変数が実数であること、つまり演算を実数に実行することを指定します。
|
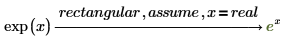 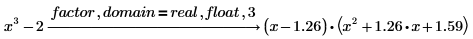 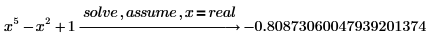 |
|
|
RealRange
|
変数が実数の範囲であることを指定します。
|
 |
|
sign
|
式を符号関数で書き換えます。
|
rewrite
|
|
signum
|
ヘビサイド関数を含む式を、数字の符号を抽出する signum 関数を使用して書き換えます。
|
rewrite
|
|
sin
|
式を正弦関数で書き換えます。
|
rewrite
|
|
sincos
|
正弦関数および余弦関数の公式を使用して式を結合または書き換えます。
|
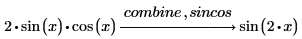 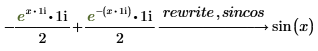 |
|
式を双曲線正弦関数で書き換えます。
|
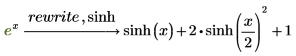 |
|
|
sinhcosh
|
双曲線正弦関数および双曲線余弦関数の公式を使用して式を結合または書き換えます。
|
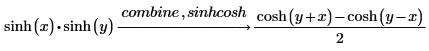 rewrite |
|
tan
|
式を正接関数で書き換えます。
|
rewrite
|
|
tanh
|
式を双曲線正接関数で書き換えます。
|
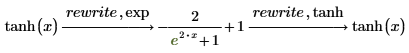 |
|
using
|
解で生成された変数を方程式に置き換えます。
|
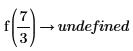 |
特殊な変更因子
変更因子 fully および using は、前にキーワードを置かないスタンドアロンのキーワードとして使用できます。キーワードと変更因子の間にコンマを追加することによって、キーワードと変更因子の有効な組み合わせを使用できます。Shift + Enter キーを押して、次の行に同じ変更因子を追加することもできます。