例: 式の因数分解および展開について
キーワード factor を使用して整数、根式、または代数式の因数分解の解を求めます。
キーワード expand を使用して、式を展開します。
整数の因数分解
1. 整数を定義します。
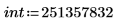
2. シンボリック評価演算子を挿入します。
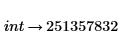
3. シンボリック評価演算子の上のプレースホルダーにキーワード factor を入力して、Enter キーを押します。
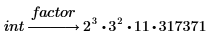
根式の因数分解
1. 根式を定義します。
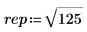
2. シンボリック評価演算子を挿入します。
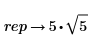
3. シンボリック評価演算子の上のプレースホルダーにキーワード factor を入力して、Enter キーを押します。
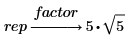
多項式の因数分解
1. x の多項式を定義します。
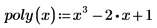
2. シンボリック評価演算子を挿入します。
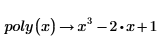
3. シンボリック評価演算子の上のプレースホルダーにキーワード factor を入力して、Enter キーを押します。
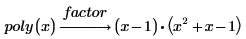
このキーワードは多項式を有理数について因数分解します。つまり、2 つの因数の係数は有理数 (整数または常分数) になります。根に 5 の平方根 (無理数) が含まれているため、2 つ目の項をこれ以上有理数で因数分解することはできません。
4. 根をベクトルで返すキーワード solve を使用して根を求めます。
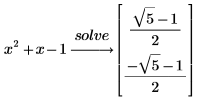
5. 元の多項式を実数にまで因数分解するには、根式である 5 の平方根を引数として追加します。これには、factor の後にコンマを入力して、コンマの後に表示されるプレースホルダーにルート 5 と入力します。
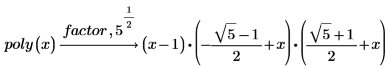
引数なしにキーワード factor を使用した場合は一般に、多項式はその係数により生成される数体に基づいて因数分解されます。つまり、多項式の係数がすべて有理数であれば、因数の係数は必ずすべて有理数になります。ただし、多項式の係数に根式が含まれる場合、因数の係数にも同じ根式が含まれる可能性があります。 |
式の展開
1. キーワード expand を使用して、次の式を展開します。
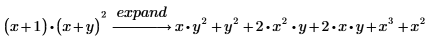
2. expand の後にコンマを入力して、主式の部分式を入力します。
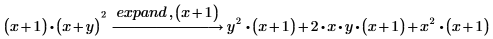
PTC Mathcad では部分式を除くすべての項が展開されます。
3. 元の式には含まれない部分式を入力します。
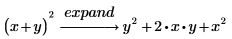
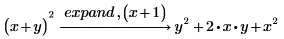
結果は、変更因子を含めない場合と同じになります。
多項式の実数までの完全因数分解
1. キーワード solve を使用して、この多項式の実数係数の実数についての解を求めます。
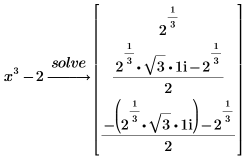
2. キーワード solve を factor に置き換えて、多項式の根に表れるすべての根式をコンマで区切って入力します。
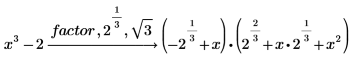
多項式を複素数まで完全に因数分解する
1. あらゆる多項式を複素数まで因数分解するには、複素数 1i を根式のリストに追加します。
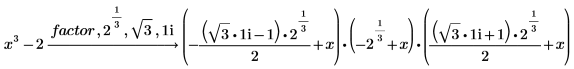
2. または、シンボリックルートによりベクトルを定義して、ベクトルのエントリを factor の後に挿入します。
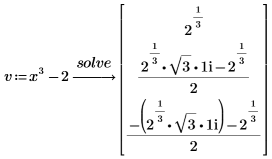
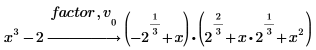
v0 には i とともに根に表れる両方の根式が含まれるため、根の 1 つを入力するだけで済みます。
3. 変更因子 real または complex を使用して、実数または複素数の多項式を、シンボリックな項でなく、浮動小数点係数を持つ項に因数分解します。
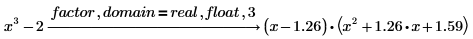
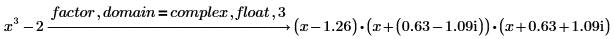
キーワード float を使用して、表示される係数の小数桁数を減らします。