例: 方程式のシンボリック解
1 つまたは複数の未知数について、方程式のシンボリックな解を求めます。
単一の方程式の求解
1. 次の方程式を入力します。
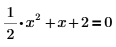
2. シンボリック評価演算子を挿入し、キーワード solve をプレースホルダーに入力して Enter キーを押します。
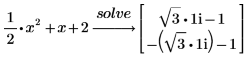
方程式の右辺は 0 なので、式の =0 の部分の入力は不要です。 |
3. 定数 2 を小数形式で 2.0 と入力すると、浮動点小数形式の解が返ります。
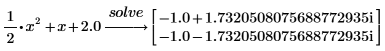
4. 1 変数方程式の解を求めます。
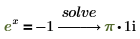
5. 多変数方程式の解を求めます。
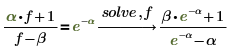
方程式に複数の変数が含まれる場合、解を求める変数を指定する必要があります。 |
6. 4 次多項式の解を求めます。

上記の結果は 4 次多項式のシンボリック解が 4 つの数値解を持つことを示します。 |
7. パラメータ化した係数について多項式の根を求めます。
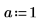
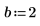
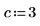
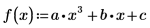
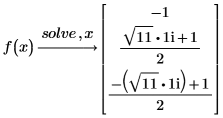
連立方程式および等式の求解
複数の方程式および等式を 1 つのベクトルにグループ化することによって連立方程式としてまとめて求解できます。
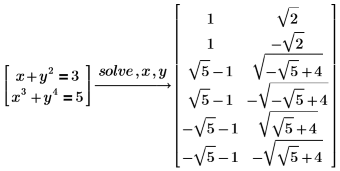
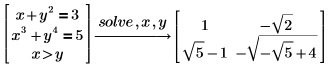
多項式の根号による求解
デフォルトで、PTC Mathcad は多項式の解を 4 乗根まで求めます。解は、根を加減乗除した形になります。
1. 次の多項式の解を求めます。
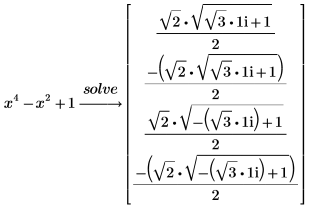
数学者のガロアは 19 世紀に、5 次以上の多項式の解は根号の形で求めることができないことを証明しました。このような多項式については、PTC Mathcad は根の数値的な近似を返します。 |
2. 5 次の多項式の解を求めます。

上記の結果は 5 次多項式のシンボリック解が 5 つの数値解を持つことを示します。 |
変数領域についての仮説を立てる
キーワード assume を使用して、設問中の変数の領域についての仮説 (実数である、など) を作成します。
1. x が実数であると仮定して方程式の解を求めます。
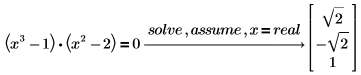
PTC Mathcad は、方程式に対して実数解のみを返します。 |
2. RealRange を使用して、範囲 (0, 2) における実数解を求めます。
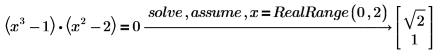
3. x=integer を入力して整数解のみを求めます。
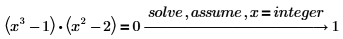
4. assume を使用して、シンボリック評価における変数の領域を制限します。
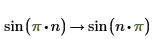
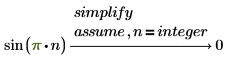
方程式の詳細解の返却
solve の後ろに変更因子 fully を追加して、方程式の詳細解を求めます。
1. 関数 clear.sym を使用して、a の以前のシンボリック値をクリアします。
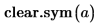
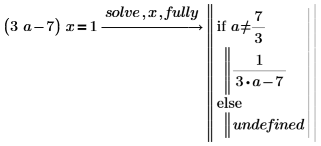
2. fully を使用して、解が有効になる a の値を返します。
3. 詳細解を使用して関数を定義します。
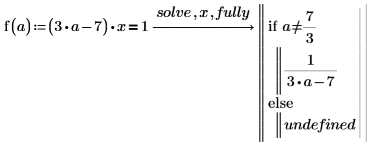
4. 関数を a=3 および a=7/3 について評価します。
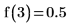
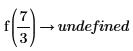
周期解を持つ方程式
周期解を持つ方程式については、PTC Mathcad は最初の解に周期式解を 1 つだけ返します。
1. fully を使用して sin(x) を評価します。
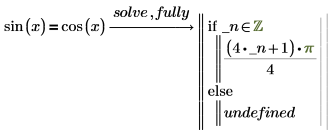
if 文に続く式は、pi/4 に pi 整数倍を加えたものであることを意味します。PTC Mathcad により、新しく生成された変数 _n が挿入されます。これは任意の整数を表します。アンダースコア (_) が生成された変数の前に付くことでワークシートの別の場所で定義されているかもしれないその他の変数との名前の重複が避けられます。 |
2. 変更因子 using を追加し、その後にブーリアンの等号を使用して記述した方程式を記述して、生成した変数が新しい変数と等しくなるよう設定します。
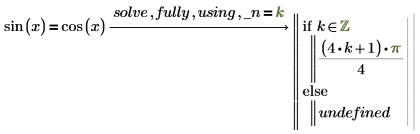
using の後に指定した変数が solve が返さない変数を生成した場合、PTC Mathcad はエラーを返します。