Modelado de transferencia de calor radiativa
En un sistema de fluido térmico, las superficies sólidas, el flujo de fluido o tanto las superficies sólidas como el flujo de fluido pueden verse sometidos a calentamiento o refrigeración debido a la radiación. En los modelos de CFA, la transferencia de calor radiativa se explica mediante la resolución de la ecuación de transporte radiativo (RTE) y la obtención del término de origen radiativo para la ecuación de conservación de energía total. Un método de modelado ampliamente utilizado, el modelo de radiación de superficie a superficie (S2S), es el modelo elegido en Creo Flow Analysis.
Ecuación de transferencia radiativa
Cuando un rayo de radiación atraviesa una capa de un medio absorbente, emisor y de dispersión en una dirección determinada, el rayo pierde energía a través de la absorción y la dispersión del rayo. El rayo también gana energía de las fuentes de luz del medio, a través de la emisión y la dispersión dirigida hacia el rayo. El balance de energía global del rayo sobre una capa infinita del medio da como resultado una ecuación diferencial, conocida como ecuación de transporte radiativo (RTE).
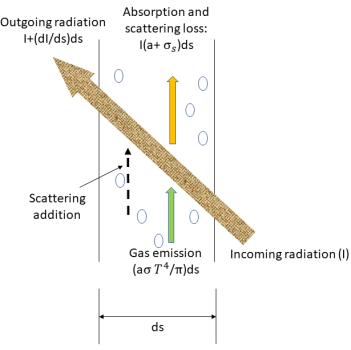
Para derivar la ecuación de transporte radiativo, se debe tener en cuenta que un rayo de radiación entrante con la intensidad I viaja a través de un medio, por ejemplo, un gas, con el espesor incremental ds en la dirección 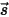 , tal como se muestra en la figura. A través de la capa del medio, la incidencia en la ubicación
, tal como se muestra en la figura. A través de la capa del medio, la incidencia en la ubicación  ⃗ y la dirección
⃗ y la dirección  cambian de cuatro maneras, lo que hace aumentar (energía ganada +) o disminuir (energía perdida -) la intensidad de radiación
cambian de cuatro maneras, lo que hace aumentar (energía ganada +) o disminuir (energía perdida -) la intensidad de radiación 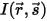 :
:
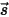 , tal como se muestra en la figura. A través de la capa del medio, la incidencia en la ubicación
, tal como se muestra en la figura. A través de la capa del medio, la incidencia en la ubicación  ⃗ y la dirección
⃗ y la dirección  cambian de cuatro maneras, lo que hace aumentar (energía ganada +) o disminuir (energía perdida -) la intensidad de radiación
cambian de cuatro maneras, lo que hace aumentar (energía ganada +) o disminuir (energía perdida -) la intensidad de radiación 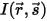 :
:• Absorción: un medio, por ejemplo, un gas, absorbe una fracción de la radiación que lo atraviesa. Con el coeficiente de absorción 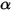 , la energía de radiación perdida por absorción es:
, la energía de radiación perdida por absorción es:
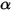 , la energía de radiación perdida por absorción es:
, la energía de radiación perdida por absorción es: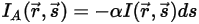
ecuación 2.282
• Dispersión: un medio, por ejemplo, un gas, dispersa una fracción de la energía de radiación hacia otra dirección (alejándola de la dirección  ) cuando el rayo atraviesa el medio. Con el coeficiente de dispersión
) cuando el rayo atraviesa el medio. Con el coeficiente de dispersión 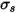 , la energía de radiación perdida por dispersión es:
, la energía de radiación perdida por dispersión es:
 ) cuando el rayo atraviesa el medio. Con el coeficiente de dispersión
) cuando el rayo atraviesa el medio. Con el coeficiente de dispersión 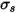 , la energía de radiación perdida por dispersión es:
, la energía de radiación perdida por dispersión es: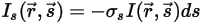
Ecuación 2.283
• Emisión: un medio emite energía de radiación hacia el rayo como cuerpo gris según su temperatura local (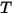 ) y las características de emisión para el rayo. Según la ley de Stefan-Boltzmann y la reciprocidad entre la emisión y la absorción, la ecuación 2.274 y la ecuación 2.279, la radiancia emitida por el medio es:
) y las características de emisión para el rayo. Según la ley de Stefan-Boltzmann y la reciprocidad entre la emisión y la absorción, la ecuación 2.274 y la ecuación 2.279, la radiancia emitida por el medio es: 
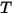 ) y las características de emisión para el rayo. Según la ley de Stefan-Boltzmann y la reciprocidad entre la emisión y la absorción, la ecuación 2.274 y la ecuación 2.279, la radiancia emitida por el medio es:
) y las características de emisión para el rayo. Según la ley de Stefan-Boltzmann y la reciprocidad entre la emisión y la absorción, la ecuación 2.274 y la ecuación 2.279, la radiancia emitida por el medio es: 
Además, suponiendo que n sea el índice de refracción del medio (definido como la relación de la velocidad de la luz en el vacío respecto a su velocidad en el medio especificado), la energía real ganada por el rayo de radiación es:
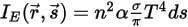
Ecuación 2.284
• Dispersión de otras radiaciones: una fracción de otros orígenes de radiación en la capa del medio se dispersa en el rayo de radiación en función de los vectores de posición y de dirección 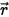 y
y 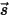 . Si se introduce
. Si se introduce 
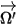 para representar la dirección y el ángulo sólido del haz de radiación y
para representar la dirección y el ángulo sólido del haz de radiación y 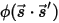 para que sea la función de fase, se obtiene la fracción de intensidad de un rayo que viaja en todas las direcciones que se dispersa hacia la dirección
para que sea la función de fase, se obtiene la fracción de intensidad de un rayo que viaja en todas las direcciones que se dispersa hacia la dirección 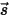 ⃗ como:
⃗ como:
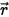 y
y 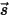 . Si se introduce
. Si se introduce 
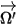 para representar la dirección y el ángulo sólido del haz de radiación y
para representar la dirección y el ángulo sólido del haz de radiación y 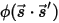 para que sea la función de fase, se obtiene la fracción de intensidad de un rayo que viaja en todas las direcciones que se dispersa hacia la dirección
para que sea la función de fase, se obtiene la fracción de intensidad de un rayo que viaja en todas las direcciones que se dispersa hacia la dirección 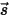 ⃗ como:
⃗ como: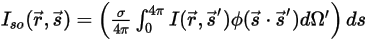
ecuación 2.285
Se debe tener en cuenta que en la ecuación 2.285, se desestiman los procesos de dispersión.
Con la radiación entrante 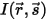 y la radiación saliente
y la radiación saliente  , el balance de energía radiativa en la dirección
, el balance de energía radiativa en la dirección  ⃗ tiene la forma:
⃗ tiene la forma:
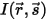 y la radiación saliente
y la radiación saliente  , el balance de energía radiativa en la dirección
, el balance de energía radiativa en la dirección  ⃗ tiene la forma:
⃗ tiene la forma: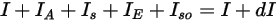
ecuación 2.286
Al sustituir la ecuación 2.282 por la ecuación 2.285 en la ecuación 2.286, y dividiéndola por 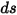 , se obtiene la ecuación de transporte radiativo (RTE), tal como se indica a continuación:
, se obtiene la ecuación de transporte radiativo (RTE), tal como se indica a continuación:
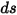 , se obtiene la ecuación de transporte radiativo (RTE), tal como se indica a continuación:
, se obtiene la ecuación de transporte radiativo (RTE), tal como se indica a continuación: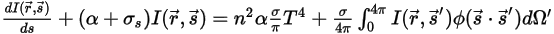
ecuación 2.287
RTE es una ecuación íntegro-diferencial de primer orden para la intensidad de la radiación 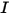 en una dirección fija
en una dirección fija 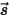 . Para resolver esta ecuación dentro de un dominio, se necesita el campo de temperatura en el dominio y también se requieren las condiciones de límite para
. Para resolver esta ecuación dentro de un dominio, se necesita el campo de temperatura en el dominio y también se requieren las condiciones de límite para  en las superficies internas y externas, así como las interfaces entre dos medios diferentes.
en las superficies internas y externas, así como las interfaces entre dos medios diferentes.
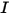 en una dirección fija
en una dirección fija 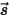 . Para resolver esta ecuación dentro de un dominio, se necesita el campo de temperatura en el dominio y también se requieren las condiciones de límite para
. Para resolver esta ecuación dentro de un dominio, se necesita el campo de temperatura en el dominio y también se requieren las condiciones de límite para  en las superficies internas y externas, así como las interfaces entre dos medios diferentes.
en las superficies internas y externas, así como las interfaces entre dos medios diferentes.La temperatura media local se obtiene al resolver la ecuación de conservación de energía total (incluidos los orígenes radiativos), que se describe en el módulo Calor (Heat). Sin embargo, para la radiación térmica, el tratamiento de los límites es complejo y depende de los modelos de radiación. En general, un límite puede ser un medio opaco que emita, refleje y absorba, o bien un medio semitransparente que también transmita. La reflexión y la transmisión pueden ser difusas o especulares, o ambas cosas. Por ejemplo, en un límite opaco de emisión y reflexión con radiación gris y, en función del tipo de reflexión, la intensidad de un rayo se puede expresar de la siguiente manera:
◦ Límite opaco con emisión y reflexión difusas:
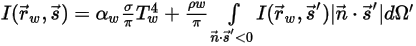
Ecuación 2.288
◦ Límite opaco con emisión difusa y reflexión especular:
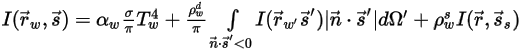
Ecuación 2.289
donde,
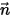 ⃗ ⃗ | vector de unidad normal a superficie en la posición  |
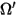 | dirección y ángulo sólido de un rayo reflejado difusamente (reflexión uniforme en todas las direcciones) |
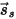 | dirección del rayo reflejado especularmente (reflexión perfecta en función de la incidencia) |
 | reflectividad de superficie, reflectividad difusa y reflectividad especular, respectivamente, que tienen la siguiente relación: 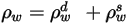 ecuación 2.290 |
Con las condiciones de límite especificadas, la ecuación 2.287 rige el transporte de la intensidad de radiación en una dirección especificada. En el caso de las radiaciones grises, la ecuación 2.287 debe resolverse en todas las direcciones diferentes dentro de una esfera. Para las radiaciones no grises, la intensidad también depende de las longitudes de onda. Por lo tanto, se debe resolver en todas las direcciones sobre todo el espectro de las longitudes de onda. Obviamente, la solución directa de la ecuación de transferencia radiativa tarda mucho tiempo. Por lo tanto, en muchas simulaciones de ingeniería, es deseable utilizar modelos simplificados, pero aproximados, para tener en cuenta las dependencias direccionales y espectrales. En simulaciones CFD, se adoptan de forma rutinaria los siguientes modelos de radiación, de los que la descripción detallada puede encontrarse en referencias.
Referencias: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modelo de radiación de Rosseland
Referencias: R, Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modelo de radiación P-1
Referencias: R. Siegel and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modelo de radiación de transferencia discreta
Referencias: N. G. Shah, "A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
Referencias: M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, Fundamentals of Radiation Heat Transfer, volumen 160, páginas 17-26. ASME HTD, 1991.
▪ Modelo de radiación de superficie a superficie (S2S)
Referencias: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modelo de radiación de ordenadas discretas (DO)
Referencias: G. D. Raithby and E. H. Chui, "A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
Referencias: E. H. Chui and G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method", Numerical Heat Transfer, Part B, 23:269-288, 1993.
Cada modelo tiene sus propias ventajas y limitaciones con respecto a la precisión y el coste. Por ejemplo, aunque el modelo de Rosseland no resuelve una ecuación de transporte para la radiación incidente, es el modelo de radiación más rápido y que requiere menos memoria adicional. Rosseland solo se puede utilizar para el espesor óptico (el espesor óptico es el logaritmo natural de la relación de potencia radiante incidente con respecto a la transmitida en un medio), debido a la excesiva simplificación de la ecuación de transporte radiativo.
El modelo de radiación de ordenadas discretas (DO) transforma la ecuación 2.287 en una ecuación de transporte para la intensidad de radiación en las coordenadas espaciales 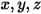 y la resuelve en un número finito de ángulos sólidos discretos asociados a la dirección del vector
y la resuelve en un número finito de ángulos sólidos discretos asociados a la dirección del vector 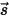 . El número de ángulos sólidos seleccionados determina directamente la precisión y el coste computacional. El enfoque de modelado de DO es idéntico también al que se utiliza para el flujo de fluido y las ecuaciones de energía. Por el momento, se trata del modelo de radiación más general que abarca todo el rango de espesores ópticos y se puede aplicar a problemas que van desde la radiación de superficie a superficie hasta la radiación participante, como un sistema de combustión. Sin embargo, el coste computacional del modelo DO es alto para las radiaciones que no son grises.
. El número de ángulos sólidos seleccionados determina directamente la precisión y el coste computacional. El enfoque de modelado de DO es idéntico también al que se utiliza para el flujo de fluido y las ecuaciones de energía. Por el momento, se trata del modelo de radiación más general que abarca todo el rango de espesores ópticos y se puede aplicar a problemas que van desde la radiación de superficie a superficie hasta la radiación participante, como un sistema de combustión. Sin embargo, el coste computacional del modelo DO es alto para las radiaciones que no son grises.
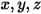 y la resuelve en un número finito de ángulos sólidos discretos asociados a la dirección del vector
y la resuelve en un número finito de ángulos sólidos discretos asociados a la dirección del vector 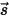 . El número de ángulos sólidos seleccionados determina directamente la precisión y el coste computacional. El enfoque de modelado de DO es idéntico también al que se utiliza para el flujo de fluido y las ecuaciones de energía. Por el momento, se trata del modelo de radiación más general que abarca todo el rango de espesores ópticos y se puede aplicar a problemas que van desde la radiación de superficie a superficie hasta la radiación participante, como un sistema de combustión. Sin embargo, el coste computacional del modelo DO es alto para las radiaciones que no son grises.
. El número de ángulos sólidos seleccionados determina directamente la precisión y el coste computacional. El enfoque de modelado de DO es idéntico también al que se utiliza para el flujo de fluido y las ecuaciones de energía. Por el momento, se trata del modelo de radiación más general que abarca todo el rango de espesores ópticos y se puede aplicar a problemas que van desde la radiación de superficie a superficie hasta la radiación participante, como un sistema de combustión. Sin embargo, el coste computacional del modelo DO es alto para las radiaciones que no son grises.Entre los modelos de radiación mencionados anteriormente, el modelo de radiación de superficie a superficie (S2S) es especialmente adecuado para modelar la transferencia radiativa del recinto, sin tener en cuenta los medios participantes. Los ejemplos típicos son los calentadores ambientales radiativos y los sistemas de automoción debajo del capó y carrocería. En estas situaciones, los modelos de radiación para la radiación participante a veces no son eficientes. En comparación con el modelo de radiación DO, el modelo S2S es más rápido por iteración, aunque el cálculo del factor de vista en sí puede requerir muchos recursos de la CPU. En Creo Flow Analysis, la elección actual del modelo para la transferencia de calor radiativa es el modelo de radiación S2S.
Modelo de radiación de superficie a superficie (S2S)
El modelo de radiación de superficie a superficie se tiene en cuenta para el intercambio de radiación en un recinto de superficies difusas grises sin medios participantes. El intercambio de energía radiativa de superficie a superficie depende de dos factores principales: las características radiativas de las superficies implicadas y los parámetros geométricos, incluidas las áreas de superficie y las formas, así como la posición relativa para llegar a otras (distancia de separación y orientación). En el modelo de radiación S2S, el modelo de radiación difusa gris toma en consideración la transferencia de calor radiativa de superficie la toma, mientras que una función geométrica denominada factor de vista tiene en cuenta los parámetros geométricos.
• Radiación difusa gris
El modelo de radiación S2S presupone que las superficies son grises y difusas (radiación gris). Para una superficie gris, tanto la emisividad 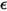 como absortividad
como absortividad 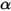 de las superficies son independientes de la longitud de onda de los rayos de salida y entrada. Según la ley de Kirchhoff de radiación térmica en la ecuación 2.274, la emisividad es igual a la absortividad:
de las superficies son independientes de la longitud de onda de los rayos de salida y entrada. Según la ley de Kirchhoff de radiación térmica en la ecuación 2.274, la emisividad es igual a la absortividad:
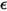 como absortividad
como absortividad 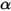 de las superficies son independientes de la longitud de onda de los rayos de salida y entrada. Según la ley de Kirchhoff de radiación térmica en la ecuación 2.274, la emisividad es igual a la absortividad:
de las superficies son independientes de la longitud de onda de los rayos de salida y entrada. Según la ley de Kirchhoff de radiación térmica en la ecuación 2.274, la emisividad es igual a la absortividad: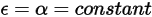
Ecuación 2.291
Asimismo, si se supone una superficie difusa, no se produce ninguna reflexión especular en la superficie y la reflectividad (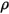 ) de la radiación incidente en la superficie es isótropa con respecto al ángulo sólido. En la ecuación 2.290, la reflectividad de superficie se determina como:
) de la radiación incidente en la superficie es isótropa con respecto al ángulo sólido. En la ecuación 2.290, la reflectividad de superficie se determina como:
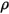 ) de la radiación incidente en la superficie es isótropa con respecto al ángulo sólido. En la ecuación 2.290, la reflectividad de superficie se determina como:
) de la radiación incidente en la superficie es isótropa con respecto al ángulo sólido. En la ecuación 2.290, la reflectividad de superficie se determina como:
Ecuación 2.292
donde,
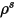 | especular de superficie |
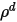 | reflectividad difusa |
Para una superficie no opaca o semitransparente, la transmisividad 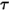 es independiente también de las longitudes de onda:
es independiente también de las longitudes de onda:
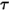 es independiente también de las longitudes de onda:
es independiente también de las longitudes de onda: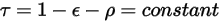
Ecuación 2.293
En el modelo de superficie a superficie difusa gris se supone que el intercambio de energía radiativa entre superficies no se ve prácticamente afectado por el medio que los separa. Por lo tanto, si una determinada cantidad de energía radiante 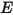 incide en una superficie por área de unidad (irradiancia), las partes de la energía radiativa reflejada, absorbida y transmitida son
incide en una superficie por área de unidad (irradiancia), las partes de la energía radiativa reflejada, absorbida y transmitida son 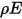
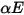 y
y 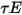 , respectivamente. Dado que, para la mayoría de las aplicaciones, las superficies son opacas para la radiación térmica en el espectro de infrarrojos, las superficies radiativas se pueden considerar como opacas. Por lo tanto, la transmisividad se puede desestimar
, respectivamente. Dado que, para la mayoría de las aplicaciones, las superficies son opacas para la radiación térmica en el espectro de infrarrojos, las superficies radiativas se pueden considerar como opacas. Por lo tanto, la transmisividad se puede desestimar 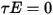 . En la ecuación 2.273 y en la ecuación 2.274, la reflectividad de superficie
. En la ecuación 2.273 y en la ecuación 2.274, la reflectividad de superficie  se expresa como:
se expresa como:
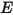 incide en una superficie por área de unidad (irradiancia), las partes de la energía radiativa reflejada, absorbida y transmitida son
incide en una superficie por área de unidad (irradiancia), las partes de la energía radiativa reflejada, absorbida y transmitida son 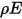
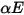 y
y 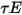 , respectivamente. Dado que, para la mayoría de las aplicaciones, las superficies son opacas para la radiación térmica en el espectro de infrarrojos, las superficies radiativas se pueden considerar como opacas. Por lo tanto, la transmisividad se puede desestimar
, respectivamente. Dado que, para la mayoría de las aplicaciones, las superficies son opacas para la radiación térmica en el espectro de infrarrojos, las superficies radiativas se pueden considerar como opacas. Por lo tanto, la transmisividad se puede desestimar 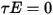 . En la ecuación 2.273 y en la ecuación 2.274, la reflectividad de superficie
. En la ecuación 2.273 y en la ecuación 2.274, la reflectividad de superficie  se expresa como:
se expresa como: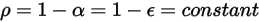
Ecuación 2.294
con las suposiciones de la radiación difusa gris de la superficie, la ecuación de modelado S2S se crea según la conservación de energía de cada superficie.
• Ecuación de modelado S2S
La suposición principal del modelo S2S es que, en un sistema cerrado, la transferencia de calor radiativa solo tiene lugar entre superficies difusas grises (radiación gris). Se puede desestimar la absorción, la emisión o la dispersión de la radiación en el medio que separa las superficies. Por lo tanto, solo se debe considerar la radiación superficie a superficie para el análisis numérico.
El flujo de energía radiativa que sale de una superficie determinada consta de la energía emitida directamente y la reflejada. El flujo de energía reflejada depende del flujo de energía incidente del entorno, que se puede expresar en términos del flujo de energía que sale de todas las demás superficies. Para calcular el flujo de energía radiativa neta en una superficie, es conveniente definir la radiosidad 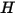 , que es la suma de la energía emisora por área de unidad (emitancia)
, que es la suma de la energía emisora por área de unidad (emitancia) 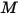 y la parte reflejada de la energía de radiación recibida por la superficie por área de unidad (irradiancia)
y la parte reflejada de la energía de radiación recibida por la superficie por área de unidad (irradiancia) 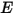 :
:
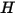 , que es la suma de la energía emisora por área de unidad (emitancia)
, que es la suma de la energía emisora por área de unidad (emitancia) 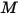 y la parte reflejada de la energía de radiación recibida por la superficie por área de unidad (irradiancia)
y la parte reflejada de la energía de radiación recibida por la superficie por área de unidad (irradiancia) 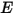 :
:
Ecuación 2.295
Para una superficie opaca, 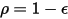 , se dispone de la radiosidad:
, se dispone de la radiosidad:
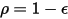 , se dispone de la radiosidad:
, se dispone de la radiosidad: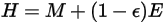
ecuación 2.296
por lo tanto, con las suposiciones en el modelo S2S, se puede formular el siguiente sistema de ecuaciones lineales para calcular la radiosidad en cada superficie de un sistema cerrado. Suponiendo que 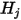 representa la radiosidad en una superficie arbitraria
representa la radiosidad en una superficie arbitraria  ,
, 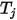 es la temperatura de la superficie y
es la temperatura de la superficie y  es el factor de vista entre la superficie
es el factor de vista entre la superficie  y
y  , se obtiene la radiosidad de la superficie
, se obtiene la radiosidad de la superficie  :
:
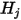 representa la radiosidad en una superficie arbitraria
representa la radiosidad en una superficie arbitraria  ,
, 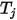 es la temperatura de la superficie y
es la temperatura de la superficie y  es el factor de vista entre la superficie
es el factor de vista entre la superficie  y
y  , se obtiene la radiosidad de la superficie
, se obtiene la radiosidad de la superficie  :
: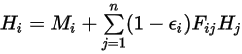
ecuación 2.297
donde 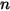 es el número de las superficies que participan en la transferencia de calor radiativa. Al introducir el símbolo de Kronecker
es el número de las superficies que participan en la transferencia de calor radiativa. Al introducir el símbolo de Kronecker 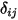 y aplicar la ley de Stefan-Boltzmann para la radiación gris, ecuación 2.278, se puede reorganizar la ecuación 2.297 y derivar la ecuación de modelado S2S:
y aplicar la ley de Stefan-Boltzmann para la radiación gris, ecuación 2.278, se puede reorganizar la ecuación 2.297 y derivar la ecuación de modelado S2S:
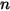 es el número de las superficies que participan en la transferencia de calor radiativa. Al introducir el símbolo de Kronecker
es el número de las superficies que participan en la transferencia de calor radiativa. Al introducir el símbolo de Kronecker 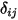 y aplicar la ley de Stefan-Boltzmann para la radiación gris, ecuación 2.278, se puede reorganizar la ecuación 2.297 y derivar la ecuación de modelado S2S:
y aplicar la ley de Stefan-Boltzmann para la radiación gris, ecuación 2.278, se puede reorganizar la ecuación 2.297 y derivar la ecuación de modelado S2S:
ecuación 2.298
Con el factor de vista calculado previamente 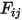 , el sistema de la ecuación 2.298 lineal se resuelve para obtener
, el sistema de la ecuación 2.298 lineal se resuelve para obtener 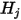 para las superficies participantes. A continuación, los flujos de calor neto de radiación de cada superficie se calculan fácilmente. Para la superficie
para las superficies participantes. A continuación, los flujos de calor neto de radiación de cada superficie se calculan fácilmente. Para la superficie  , el flujo térmico radiativo neto
, el flujo térmico radiativo neto 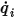 es la diferencia entre la radiación saliente (
es la diferencia entre la radiación saliente (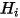 ) y la entrante (
) y la entrante (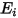 ) por área de unidad. De la ecuación 2.278 y la ecuación 2.296, se puede derivar la siguiente formulación de flujo:
) por área de unidad. De la ecuación 2.278 y la ecuación 2.296, se puede derivar la siguiente formulación de flujo:
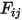 , el sistema de la ecuación 2.298 lineal se resuelve para obtener
, el sistema de la ecuación 2.298 lineal se resuelve para obtener 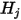 para las superficies participantes. A continuación, los flujos de calor neto de radiación de cada superficie se calculan fácilmente. Para la superficie
para las superficies participantes. A continuación, los flujos de calor neto de radiación de cada superficie se calculan fácilmente. Para la superficie  , el flujo térmico radiativo neto
, el flujo térmico radiativo neto 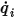 es la diferencia entre la radiación saliente (
es la diferencia entre la radiación saliente (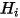 ) y la entrante (
) y la entrante (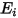 ) por área de unidad. De la ecuación 2.278 y la ecuación 2.296, se puede derivar la siguiente formulación de flujo:
) por área de unidad. De la ecuación 2.278 y la ecuación 2.296, se puede derivar la siguiente formulación de flujo: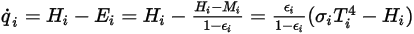
Ecuación 2.299
Para un área de superficie determinada 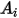 , los flujos térmicos de radiación neta que salen de la superficie
, los flujos térmicos de radiación neta que salen de la superficie 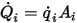 se calculan de la siguiente manera:
se calculan de la siguiente manera:
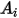 , los flujos térmicos de radiación neta que salen de la superficie
, los flujos térmicos de radiación neta que salen de la superficie 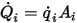 se calculan de la siguiente manera:
se calculan de la siguiente manera: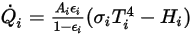
Ecuación 2.300
El modelo S2S se compone de un sistema de ecuaciones lineales en forma de la ecuación 2.298. La ventaja de la aplicación del modelo es que, para los factores de vista y las temperaturas dados, los flujos de calor neto se calculan mediante la resolución de un sistema de ecuaciones lineales, que se calcula mediante la aplicación de algoritmos numéricos. Sin embargo, la dificultad principal para aplicar el modelo de superficie a superficie propuesto es el cálculo de los factores de vista 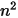 , para un número n de superficies participantes. Esto puede tardar mucho tiempo, en particular, con un aumento del número de superficies.
, para un número n de superficies participantes. Esto puede tardar mucho tiempo, en particular, con un aumento del número de superficies.
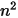 , para un número n de superficies participantes. Esto puede tardar mucho tiempo, en particular, con un aumento del número de superficies.
, para un número n de superficies participantes. Esto puede tardar mucho tiempo, en particular, con un aumento del número de superficies.Cálculo del factor de vista
En la ecuación 2.298 del modelado S2S, el factor de vista 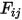 es la proporción de la radiación que sale de la superficie
es la proporción de la radiación que sale de la superficie  y alcanza la superficie
y alcanza la superficie  . Como se muestra en la figura 2.37, suponiendo que
. Como se muestra en la figura 2.37, suponiendo que 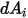 es el área diferencial de la superficie
es el área diferencial de la superficie  ,
, 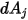 es el área diferencial de la superficie
es el área diferencial de la superficie 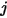 y la distancia entre
y la distancia entre 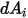 , y
, y 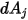 es
es 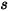 , el factor de vista
, el factor de vista 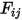 de
de 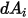 a
a 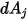 a una distancia
a una distancia 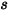 se expresa tal como se indica a continuación:
se expresa tal como se indica a continuación:
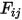 es la proporción de la radiación que sale de la superficie
es la proporción de la radiación que sale de la superficie  y alcanza la superficie
y alcanza la superficie  . Como se muestra en la figura 2.37, suponiendo que
. Como se muestra en la figura 2.37, suponiendo que 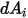 es el área diferencial de la superficie
es el área diferencial de la superficie  ,
, 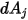 es el área diferencial de la superficie
es el área diferencial de la superficie 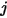 y la distancia entre
y la distancia entre 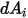 , y
, y 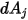 es
es 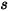 , el factor de vista
, el factor de vista 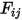 de
de 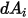 a
a 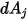 a una distancia
a una distancia 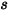 se expresa tal como se indica a continuación:
se expresa tal como se indica a continuación: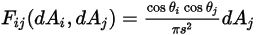
ecuación 2.301
donde 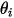 y
y  son el ángulo entre las direcciones normales a la superficie y un rayo entre las dos áreas diferenciales.
son el ángulo entre las direcciones normales a la superficie y un rayo entre las dos áreas diferenciales.
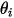 y
y  son el ángulo entre las direcciones normales a la superficie y un rayo entre las dos áreas diferenciales.
son el ángulo entre las direcciones normales a la superficie y un rayo entre las dos áreas diferenciales.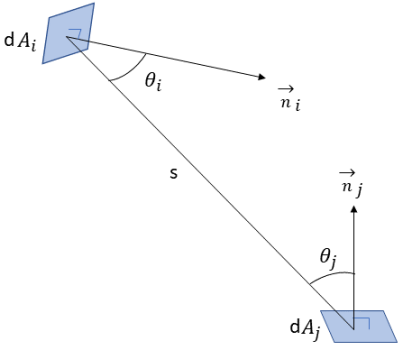
Figura 2.37
Si 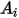 y
y 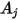 son las áreas de superficie especificadas
son las áreas de superficie especificadas  y
y 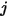 , respectivamente, el factor de vista de la superficie
, respectivamente, el factor de vista de la superficie  a la superficie
a la superficie 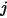 es la integral media de área de la ecuación 2.301 en las superficies
es la integral media de área de la ecuación 2.301 en las superficies  y
y 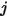 :
:
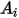 y
y 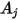 son las áreas de superficie especificadas
son las áreas de superficie especificadas  y
y 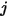 , respectivamente, el factor de vista de la superficie
, respectivamente, el factor de vista de la superficie  a la superficie
a la superficie 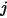 es la integral media de área de la ecuación 2.301 en las superficies
es la integral media de área de la ecuación 2.301 en las superficies  y
y 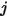 :
: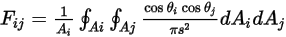
ecuación 2.302
Se debe tener en cuenta que la radiación de superficie a superficie solo se produce cuando las dos superficies son visibles entre sí, o el factor de vista es distinto de cero. Introducción del símbolo de Kronecker 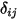 con respecto a la visibilidad entre
con respecto a la visibilidad entre 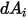 y
y 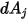 :
:
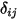 con respecto a la visibilidad entre
con respecto a la visibilidad entre 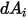 y
y 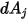 :
: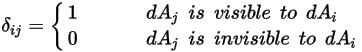
Ecuación 2.303
se puede reescribir la ecuación 2.302 como:
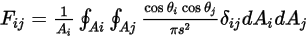
Ecuación 2.304
Para dos superficies visibles entre sí, una superficie determinada  solo irradiará una parte de la energía radiativa saliente a la superficie
solo irradiará una parte de la energía radiativa saliente a la superficie 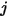 , tal como se muestra en la figura 2.378. Por lo tanto, el factor de vista sin cotas
, tal como se muestra en la figura 2.378. Por lo tanto, el factor de vista sin cotas 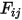 representa la parte de energía que sale de la superficie
representa la parte de energía que sale de la superficie  y alcanza la superficie
y alcanza la superficie 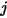 . Las características se encuentran en la lista siguiente:
. Las características se encuentran en la lista siguiente:
 solo irradiará una parte de la energía radiativa saliente a la superficie
solo irradiará una parte de la energía radiativa saliente a la superficie 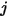 , tal como se muestra en la figura 2.378. Por lo tanto, el factor de vista sin cotas
, tal como se muestra en la figura 2.378. Por lo tanto, el factor de vista sin cotas 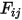 representa la parte de energía que sale de la superficie
representa la parte de energía que sale de la superficie  y alcanza la superficie
y alcanza la superficie 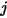 . Las características se encuentran en la lista siguiente:
. Las características se encuentran en la lista siguiente: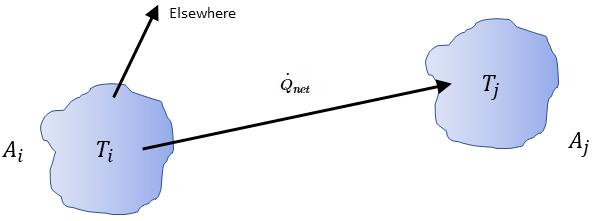
Figura 2.378
• Suma de factores de vista: puesto que se conserva la radiación que sale de una superficie, la suma de todos los factores de vista de una superficie determinada  es la unidad. Para el sistema cerrado de superficie
es la unidad. Para el sistema cerrado de superficie 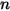 , hay
, hay
 es la unidad. Para el sistema cerrado de superficie
es la unidad. Para el sistema cerrado de superficie 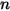 , hay
, hay
Ecuación 2.305
• Superficies de vista propia: puesto que la radiación viaja en línea recta, ningún rayo de radiación de una superficie convexa puede salir de la superficie y luego incidir en la misma superficie. Por lo tanto, las superficies convexas no se pueden ver a sí mismas:
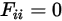
Ecuación 2.306
Para superficies cóncavas, el rayo saliente de una posición de la superficie puede incidir en la misma superficie posteriormente en otra posición. Por lo tanto, la superficie cóncava puede ser visible para sí misma:
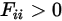
Ecuación 2.307
• Superposición: en el sistema de superficies 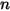 , si una superficie determinada
, si una superficie determinada  irradia a un número de superficies
irradia a un número de superficies 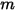 (
( ), el factor de vista entre la superficie
), el factor de vista entre la superficie  y el número
y el número 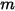 de superficies es igual a la suma de los factores de vista entre la superficie
de superficies es igual a la suma de los factores de vista entre la superficie  y cada número
y cada número 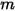 de superficies:
de superficies:
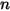 , si una superficie determinada
, si una superficie determinada  irradia a un número de superficies
irradia a un número de superficies 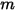 (
( ), el factor de vista entre la superficie
), el factor de vista entre la superficie  y el número
y el número 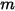 de superficies es igual a la suma de los factores de vista entre la superficie
de superficies es igual a la suma de los factores de vista entre la superficie  y cada número
y cada número 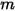 de superficies:
de superficies: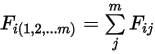
Ecuación 2.308
La regla de superposición o la regla de suma es útil cuando una geometría no está disponible con gráficos determinados. Con la regla de superposición, la geometría que se busca se puede expresar utilizando la suma o la resta de geometrías conocidas.
• Reciprocidad: la ecuación 2.304 define el factor de vista 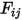 como la fracción de la energía radiativa que sale de la superficie
como la fracción de la energía radiativa que sale de la superficie  y alcanza la superficie
y alcanza la superficie 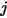 . Del mismo modo, el factor de vista
. Del mismo modo, el factor de vista  que es la parte de energía que sale de la superficie
que es la parte de energía que sale de la superficie 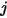 y alcanza la superficie
y alcanza la superficie  , se expresa como:
, se expresa como:
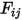 como la fracción de la energía radiativa que sale de la superficie
como la fracción de la energía radiativa que sale de la superficie  y alcanza la superficie
y alcanza la superficie 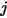 . Del mismo modo, el factor de vista
. Del mismo modo, el factor de vista  que es la parte de energía que sale de la superficie
que es la parte de energía que sale de la superficie 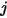 y alcanza la superficie
y alcanza la superficie  , se expresa como:
, se expresa como: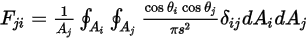
Ecuación 2.309
Si se compara la ecuación 2.309 con la ecuación 2.304, se obtiene la siguiente relación:

Ecuación 2.310
La ecuación 2.310 se conoce como la reciprocidad de los factores de vista. Con el teorema de reciprocidad, se puede calcular directamente solo uno de los valores del par de factores de vista.
Agrupación
El modelo de radiación S2S es costoso desde el punto de vista computacional cuando el número de superficies radiantes es elevado. Para reducir el tiempo computacional y el requisito de almacenamiento, se puede reducir el número de superficies radiantes agrupando un determinado número de caras de celda de límite contiguas para crear clústeres de superficie. A continuación, se calcula la radiosidad (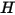 ) para los clústeres de superficie. Después, estos valores se distribuyen a las caras de celda de límite de cada clúster para calcular las temperaturas de pared. Puesto que los términos de origen de radiación son altamente no lineales (proporcionales a la cuarta potencia de temperatura), asegúrese de calcular la temperatura media de los clústeres de superficie y distribuir los términos de flujo y origen correctamente entre las caras de límite que forman los clústeres.
) para los clústeres de superficie. Después, estos valores se distribuyen a las caras de celda de límite de cada clúster para calcular las temperaturas de pared. Puesto que los términos de origen de radiación son altamente no lineales (proporcionales a la cuarta potencia de temperatura), asegúrese de calcular la temperatura media de los clústeres de superficie y distribuir los términos de flujo y origen correctamente entre las caras de límite que forman los clústeres.
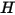 ) para los clústeres de superficie. Después, estos valores se distribuyen a las caras de celda de límite de cada clúster para calcular las temperaturas de pared. Puesto que los términos de origen de radiación son altamente no lineales (proporcionales a la cuarta potencia de temperatura), asegúrese de calcular la temperatura media de los clústeres de superficie y distribuir los términos de flujo y origen correctamente entre las caras de límite que forman los clústeres.
) para los clústeres de superficie. Después, estos valores se distribuyen a las caras de celda de límite de cada clúster para calcular las temperaturas de pared. Puesto que los términos de origen de radiación son altamente no lineales (proporcionales a la cuarta potencia de temperatura), asegúrese de calcular la temperatura media de los clústeres de superficie y distribuir los términos de flujo y origen correctamente entre las caras de límite que forman los clústeres.La temperatura del clúster de superficie se obtiene calculando la media del área de la temperatura de la cara de límite, tal como se muestra en la siguiente ecuación:

Ecuación 2.311
donde  es la temperatura del clúster de superficie, y
es la temperatura del clúster de superficie, y 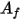 y
y 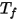 son el área de cara y la temperatura de la celda de límite en simulaciones CFA. La suma se realiza en todas las caras de un clúster de superficie.
son el área de cara y la temperatura de la celda de límite en simulaciones CFA. La suma se realiza en todas las caras de un clúster de superficie.
 es la temperatura del clúster de superficie, y
es la temperatura del clúster de superficie, y 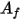 y
y 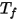 son el área de cara y la temperatura de la celda de límite en simulaciones CFA. La suma se realiza en todas las caras de un clúster de superficie.
son el área de cara y la temperatura de la celda de límite en simulaciones CFA. La suma se realiza en todas las caras de un clúster de superficie.