Características de la radiación térmica
Las características de la radiación térmica dependen de las siguientes propiedades del objeto o cuerpo emisor:
• Temperatura de superficie
• Suavidad o rugosidad de la superficie
• Absortividad espectral
• Energía emisora espectral
Como ondas electromagnéticas, la radiación térmica consta de una dispersión continua de energías de fotón con un espectro de frecuencias o longitudes de onda. Para un cuerpo emisor, la distribución del espectro, el valor máximo de la longitud de onda y la cantidad total de todas las longitudes de onda irradiadas varían según la temperatura de la superficie del cuerpo emisor. A su vez, a una temperatura de superficie determinada, la absortividad, la reflectividad y la emisividad del cuerpo emisor son dependientes de la longitud de onda de la radiación.
Intercambio de energía radiativa
Todos los cuerpos irradian energía en forma de fotones que se mueven en dirección aleatoria, con una fase y frecuencia aleatorias. Cuando los fotones irradiados desde la superficie de un cuerpo alcanzan la superficie de otro cuerpo, como se muestra en la figura 2.35, pueden ser absorbidos, reflejados y/o transmitidos. El comportamiento de una superficie con una incidencia de radiación se puede describir mediante las siguientes cantidades.
Referencias: R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
• Absorbancia α: fracción de radiación incidente absorbida a una longitud de onda determinada.
• Reflectancia ρ: fracción de radiación incidente reflejada a una longitud de onda determinada.
• Transmitancia τ: fracción de radiación incidente que se transmite a una longitud de onda determinada.
Los tres coeficientes son funciones de la longitud de onda de las ondas electromagnéticas en radiación λ. De las consideraciones de energía se deduce que deben sumar la unidad:
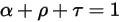
ecuación 2.273
Según la ley de la radiación térmica de Kirchhoff, la emisividad de un cuerpo emisor es igual a la absortividad espectral para cualquier longitud de onda determinada debido a la reciprocidad:
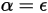
ecuación 2.274
donde ε es la emisividad, la proporción de la energía irradiada de un cuerpo emisor con respecto a la de un emisor perfecto (cuerpo negro) con la misma temperatura y longitud de onda.
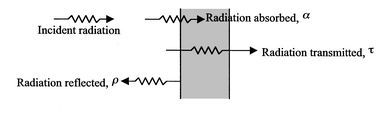
Figura 2.35
La ecuación 2.273 indica que el comportamiento de cómo un cuerpo reacciona en relación con la radiación térmica se caracteriza por su absorción α, reflexión ρ y transmisión τ. En función de los valores de α, ρ y τ, se definen los siguientes tipos ideales del cuerpo emisor:
R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• Cuerpo opaco: no transmite ninguna radiación que le alcanza, pero puede reflejar alguna radiación. τ = 0 y α + ρ = 1
• Cuerpo transparente: transmite toda la radiación que le alcanza. τ = 1 y α = ρ = 0
• Cuerpo negro: modelo teórico propuesto por Planck. El cuerpo negro es un objeto que absorba toda la radiación electromagnética incidente en todas las longitudes de onda, independientemente de la frecuencia o el ángulo de incidencia. Si un objeto de emisión de radiación cumple las características físicas de un cuerpo negro en equilibrio termodinámico, la radiación se denomina radiación de cuerpo negro. Para un cuerpo negro, α = ε 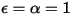 y
y 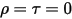
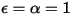 y
y 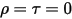
• Cuerpo blanco: se presupone que todos los rayos incidentes se reflejan completa y uniformemente en todas las direcciones. 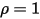 y
y 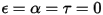
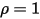 y
y 
• Cuerpo gris: cuerpo para el que  y
y  son independientes de la temperatura y la longitud de onda.
son independientes de la temperatura y la longitud de onda.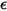 es uniforme para todas las longitudes de onda. La radiación de un cuerpo o una superficie gris se denomina radiación gris. A diferencia de la radiación gris, la radiación térmica con un espectro de longitudes de onda se conoce como radiación no gris.
es uniforme para todas las longitudes de onda. La radiación de un cuerpo o una superficie gris se denomina radiación gris. A diferencia de la radiación gris, la radiación térmica con un espectro de longitudes de onda se conoce como radiación no gris.
 y
y  son independientes de la temperatura y la longitud de onda.
son independientes de la temperatura y la longitud de onda.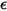 es uniforme para todas las longitudes de onda. La radiación de un cuerpo o una superficie gris se denomina radiación gris. A diferencia de la radiación gris, la radiación térmica con un espectro de longitudes de onda se conoce como radiación no gris.
es uniforme para todas las longitudes de onda. La radiación de un cuerpo o una superficie gris se denomina radiación gris. A diferencia de la radiación gris, la radiación térmica con un espectro de longitudes de onda se conoce como radiación no gris.Energía radiativa
• Energía 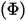 : la energía radiativa total o neta emitida, reflejada, transmitida o recibida por unidad de tiempo para un origen determinado.
: la energía radiativa total o neta emitida, reflejada, transmitida o recibida por unidad de tiempo para un origen determinado.
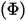 : la energía radiativa total o neta emitida, reflejada, transmitida o recibida por unidad de tiempo para un origen determinado.
: la energía radiativa total o neta emitida, reflejada, transmitida o recibida por unidad de tiempo para un origen determinado.• Irradiación (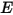 ): potencia de radiación recibida por una superficie
): potencia de radiación recibida por una superficie 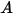 por área de unidad.
por área de unidad. 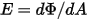
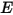 ): potencia de radiación recibida por una superficie
): potencia de radiación recibida por una superficie 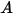 por área de unidad.
por área de unidad. 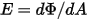
• Emitancia ( ): energía de radiación emitida
): energía de radiación emitida 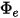 por una superficie por área de unidad.
por una superficie por área de unidad. 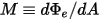
 ): energía de radiación emitida
): energía de radiación emitida 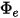 por una superficie por área de unidad.
por una superficie por área de unidad. 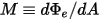
• Intensidad (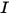 ): energía irradiada en una dirección determinada (ángulo sólido
): energía irradiada en una dirección determinada (ángulo sólido 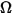 ) para un origen determinado.
) para un origen determinado. 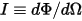
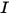 ): energía irradiada en una dirección determinada (ángulo sólido
): energía irradiada en una dirección determinada (ángulo sólido 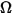 ) para un origen determinado.
) para un origen determinado. 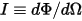
• Radiancia (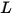 ): energía radiante emitida, reflejada, transmitida o recibida por una superficie determinada, por ángulo sólido de unidad por área proyectada de unidad.
): energía radiante emitida, reflejada, transmitida o recibida por una superficie determinada, por ángulo sólido de unidad por área proyectada de unidad. 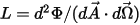
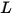 ): energía radiante emitida, reflejada, transmitida o recibida por una superficie determinada, por ángulo sólido de unidad por área proyectada de unidad.
): energía radiante emitida, reflejada, transmitida o recibida por una superficie determinada, por ángulo sólido de unidad por área proyectada de unidad. 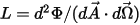
• Ley de Planck
La radiación térmica que emite un cuerpo a cualquier temperatura consta de un amplio rango de frecuencias. En el caso de un cuerpo negro, la ley de Planck describe la distribución de frecuencias de la radiación del cuerpo negro como solo la función de la temperatura del objeto. Planck demostró que la radiancia espectral de un cuerpo negro, 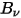 , definida como la energía emitida por área de unidad del cuerpo, por ángulo sólido de unidad en el que se mide la radiación y por frecuencia de unidad,
, definida como la energía emitida por área de unidad del cuerpo, por ángulo sólido de unidad en el que se mide la radiación y por frecuencia de unidad, 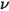 , tiene la formulación correspondiente a la temperatura del cuerpo:
, tiene la formulación correspondiente a la temperatura del cuerpo:
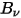 , definida como la energía emitida por área de unidad del cuerpo, por ángulo sólido de unidad en el que se mide la radiación y por frecuencia de unidad,
, definida como la energía emitida por área de unidad del cuerpo, por ángulo sólido de unidad en el que se mide la radiación y por frecuencia de unidad, 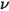 , tiene la formulación correspondiente a la temperatura del cuerpo:
, tiene la formulación correspondiente a la temperatura del cuerpo:
Ecuación 2.275
donde,
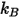 | Constante de Boltzmann |
h | Constante de Planck |
c | velocidad de la luz en el vacío o un medio material |
La radiancia espectral también se expresa por longitud de onda de unidad, λ:
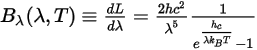
Ecuación 2.276
• Ley de Stefan-Boltzmann:
A través de la integración de la ley de Planck sobre la frecuencia, v, la salida de energía proporcionada por la ley de Stefan-Boltzmann es la energía emitida desde un cuerpo negro desde el punto de vista de su temperatura. La ley de Stefan-Boltzmann también se conoce como la emitancia radiante del cuerpo negro. La ley de Stefan-Boltzmann establece que la energía total irradiada por área de superficie de unidad de un cuerpo negro a través de todas las longitudes de onda por unidad de tiempo es directamente proporcional a la temperatura termodinámica del cuerpo negro elevada a la cuarta potencia.  :
:
 :
: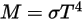
2.277
donde,
σ | Constante de Stefan-Boltzmann |
M | emitancia radiante |
En el caso de un cuerpo gris, que no absorbe toda la radiación incidente, emite menos energía total que un cuerpo negro. Con la introducción de la emisividad,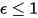 (cuerpo negro:
(cuerpo negro: 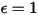 ), la ecuación 2.277 se extiende al cuerpo gris:
), la ecuación 2.277 se extiende al cuerpo gris:
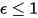 (cuerpo negro:
(cuerpo negro: 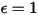 ), la ecuación 2.277 se extiende al cuerpo gris:
), la ecuación 2.277 se extiende al cuerpo gris: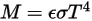
2.278
De la ley de Stefan-Boltzmann, se deduce que la radiancia y la energía emitidas por un cuerpo se calculan de la siguiente manera:

ecuación 2.279
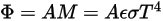
Ecuación 2.280
• Ley de desplazamiento de Wien
La ley de desplazamiento de Wien indica que la longitud de onda λ, para la que la radiancia espectral de una radiación de cuerpo negro por longitud de onda de unidad alcanza su valor máximo, es inversamente proporcional a la temperatura:
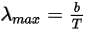
Ecuación 2.281
donde b es la constante de desplazamiento de Wien.
Constantes de modelo
Las constantes de modelo utilizadas en los modelos teóricos anteriores se indican en la siguiente tabla:
h | Constante de Planck | 6.626 069 3(11) ×10-34J-s = 4.135 667 43(35) ×10-15eV-s |
b | Constante de desplazamiento de Wien | 2.897 768 5(51) ×10-3m-K |
kB | Constante de Boltzmann | 1.380 650 5(24) ×10-23J/K = 8.617 343 (15) ×10-5eV/K |
σ | Constante de Stefan-Boltzmann | 5.670 373 (21) ×10-8 W/(m2-K4) |
c | Velocidad de la luz | 299 792 458 m/s |