Considerazioni numeriche
Nei modelli multifase omogenei, senza considerare gli slittamenti di velocità, non è necessario alcun trattamento speciale per risolvere le equazioni del momento della miscela e la formula del flusso del volume della faccia. Questo perché sono le stesse equazioni che regolano i flussi monofase a densità variabile. In questa sezione viene descritta la costruzione dell'equazione di correzione della pressione e il trattamento delle equazioni della frazione del volume di fase, in particolare dell'interfaccia che risolve gli schemi nel modello VOF.
Equazione di continuità del volume
Per soddisfare il vincolo di continuità e garantire la stabilità numerica, l'equazione di correzione della pressione è costruita sulla base della continuità del volume totale invece della continuità di massa. Quando dividete la q-esima frazione continuità di fase/volume, ovvero l'equazione 2.57 per una densità di riferimento di fase , ρrq, e combinate tutte le fasi insieme, riceverete un'equazione di continuità totale del volume che soddisfa la legge di conservazione di massa:
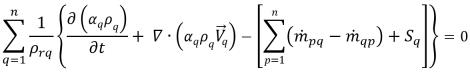
equazione 2.135
dove la densità di riferimento della fase in genere viene impostata come la densità di fase, ρrq = ρq
Introducendo Ω come il volume della cella di calcolo e integrando l'equazione 2.135 sul volume di controllo, vengono generate le equazioni algebriche discretizzate di seguito.
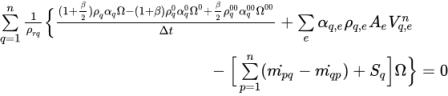
equazione 2.136
Se utilizzate lo stesso approccio risolutivo basato sulla pressione monofase descritto nella sezione Valori numerici e si assume:
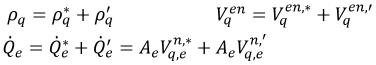
equazione 2.137
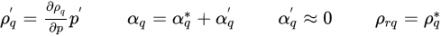
equazione 2.138
potete ridisporre l'equazione 2.136 come la seguente equazione di correzione:
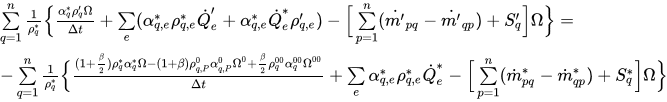
equazione 2.139
Qui * e ' rappresentano i vecchi valori e le relative correzioni.
Δt | passo temporale |
Ae | area sulla faccia e |
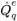 | flusso di volume |
Seguendo lo stesso approccio del solutore basato sulla pressione monofase, applicare il tipo di algoritmi SIMPLE (Simple, SimpleC e SimpleS) per connettere le correzioni di velocità e pressione e per ottenere l'equazione di correzione della pressione per i flussi multifase.
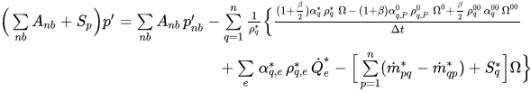
equazione 2.140
dove
Anb | coefficiente di collegamento |
Sp | termine linearizzato |
Equazioni della frazione di volume di fase
Il trasporto di una frazione di volume di fase viene regolato dalla conservazione della massa della fase. Poiché la conservazione del volume totale viene applicata nella formazione dell'equazione di correzione della pressione, le equazioni effettive risolte per frazioni di volume di fase saranno anch'esse sotto forma di conservazione del volume per la coerenza numerica:
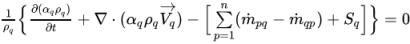
equazione 2.141
In genere, per un sistema a n fasi, vengono risolte solo le (n-1) equazioni mentre la n-esima fase viene ottenuta dal vincolo fisico:
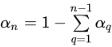
equazione 2.142
Seguendo lo stesso approccio di discretizzazione, la forma integrale dell'equazione 2.141 è la seguente:
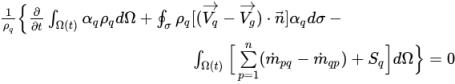
equazione 2.143
Come indicato nelle equazioni di conservazione di momento, energia e volume totale, gli schemi di discretizzazione spaziale e temporale sono fondamentali per la precisione numerica. Per le equazioni della frazione di volume, oltre agli schemi temporali impliciti standard, è prassi comune utilizzare la marcia del tempo esplicita con schemi di risoluzione ad alta risoluzione in modo da poter acquisire le interfacce nei modelli VOF in modo più preciso. Entrambe le formulazioni VOF implicite ed esplicite sono descritte in dettaglio in questa sezione.
• Formulazione VOF implicita
Con la formulazione VOF implicita, l'equazione della frazione del volume di fase discretizzata ha l'espressione generale riportata di seguito.
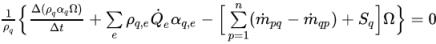
equazione 2.144
In questa equazione, la frazione di volume di fase αq nel passo temporale corrente è funzione di altre quantità nel passo. Pertanto, come indicato nelle equazioni di correzione di momento, energia e pressione, la frazione di volume discretizzato equazione 2.144 è risolta in maniera iterativa per ciascun passo temporale. In Creo Flow Analysis, la formulazione implicita adottata è riepilogata come riportato di seguito.
◦ Schemi di avvezione - Il flusso volumetrico 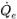 viene calcolato in base al campo di flusso nel passo temporale corrente. Il valore della faccia αq,e è approssimato in funzione dei valori centrali della cella αq,P,αq,E e dei gradienti (
viene calcolato in base al campo di flusso nel passo temporale corrente. Il valore della faccia αq,e è approssimato in funzione dei valori centrali della cella αq,P,αq,E e dei gradienti (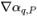 ,
,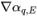 ) delle celle vicine P ed E. Come nell'equazione scalare passiva, gli schemi di avvezione hanno la forma generale:
) delle celle vicine P ed E. Come nell'equazione scalare passiva, gli schemi di avvezione hanno la forma generale:
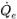 viene calcolato in base al campo di flusso nel passo temporale corrente. Il valore della faccia αq,e è approssimato in funzione dei valori centrali della cella αq,P,αq,E e dei gradienti (
viene calcolato in base al campo di flusso nel passo temporale corrente. Il valore della faccia αq,e è approssimato in funzione dei valori centrali della cella αq,P,αq,E e dei gradienti (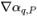 ,
,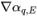 ) delle celle vicine P ed E. Come nell'equazione scalare passiva, gli schemi di avvezione hanno la forma generale:
) delle celle vicine P ed E. Come nell'equazione scalare passiva, gli schemi di avvezione hanno la forma generale: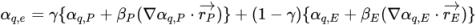
equazione 2.145
Utilizzando valori diversi per i parametri γ, βP e βE e gli schemi per calcolare i gradienti delle frazioni di volume, sono stati sviluppati quattro schemi di avvezione per le equazioni di frazione di volume: First-Order Upwind, Second-Order Upwind, Center Difference e High Resolution.
◦ Schemi temporali - Per descrivere lo schema temporale implicito, potete generalizzare l'equazione 2.144 nell'espressione riportata di seguito.
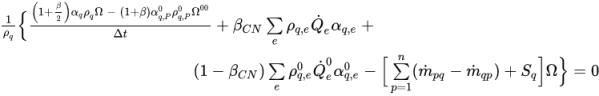
equazione 2.146
Le variabili senza un apice sono i valori nel passo temporale corrente. Le variabili con l'apice 0 o 00 indicano i valori ai passi temporali precedenti.
I parametri β e βCN variano tra 0 e 1 e determinano gli schemi temporali. In particolare, per la discretizzazione delle equazioni delle frazioni di volumi di fase vengono adottati i tre schemi temporali riportati di seguito.
▪ Euler First-Order Upwind: β = 0, βCN = 1
▪ Three-Level Second-Order: β = 0, βCN = 1
▪ Metodo Crank-Nicolson: β = 0, βCN = 0,6 (default)
• Formulazione VOF esplicita
Quando la formulazione esplicita viene utilizzata per risolvere le equazioni VOF, le frazioni di volume di fase nel passo temporale corrente vengono calcolate direttamente in base alle quantità note dal passo temporale precedente. Di conseguenza, la formulazione VOF esplicita non richiede una soluzione iterativa per l'equazione 2.144 durante ciascun passo temporale. Tuttavia, poiché il resto di equazioni di trasporto viene risolto in modo implicito, il passo temporale utilizzato per il calcolo della frazione di volume sarà in genere inferiore al passo temporale utilizzato per le altre equazioni di trasporto. È necessario determinare un passo temporale secondario per la formulazione VOF esplicita, che viene calcolata automaticamente o che è possibile fornire in Creo Flow Analysis.
Con la formulazione esplicita, l'equazione della frazione di volume di fase viene formulata come:
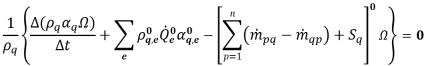
equazione 2.147
dove sia i termini di origine che di avvezione sono calcolati in base alle quantità note dal passo temporale precedente. Il flusso volumetrico 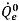 viene calcolato come
viene calcolato come 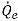 nella formulazione implicita. La frazione di volume della faccia
nella formulazione implicita. La frazione di volume della faccia 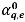 può essere stimata anche utilizzando uno dei quattro schemi di avvezione: First-Order Upwind, Second-Order Upwind, Center Difference e High Resolution.
può essere stimata anche utilizzando uno dei quattro schemi di avvezione: First-Order Upwind, Second-Order Upwind, Center Difference e High Resolution.
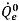 viene calcolato come
viene calcolato come 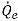 nella formulazione implicita. La frazione di volume della faccia
nella formulazione implicita. La frazione di volume della faccia 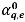 può essere stimata anche utilizzando uno dei quattro schemi di avvezione: First-Order Upwind, Second-Order Upwind, Center Difference e High Resolution.
può essere stimata anche utilizzando uno dei quattro schemi di avvezione: First-Order Upwind, Second-Order Upwind, Center Difference e High Resolution.Creo Flow Analysis offre i tre algoritmi per gli schemi di associazione temporale espliciti riportati di seguito.
• Eulero (Euler) First Order Explicit - L'equazione di frazione di volume è discretizzata nel modo seguente:
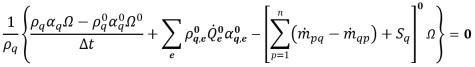
equazione 2.148
• Runge-Kutta Second-Order - Introduce la funzione:
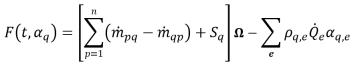
equazione 2.149
l'equazione 2.147 viene riscritta come segue:
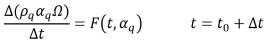
equazione 2.150
Quindi lo schema esplicito Runge-Kutta di secondo ordine ha il formato:
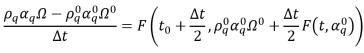
equazione 2.151
• Runge-Kutta Fourth-Order - Per l'equazione della frazione di volume a q fasi, lo schema esplicito Runge-Kutta di quarto ordine ha il formato:
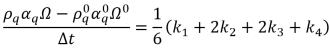
equazione 2.152
dove:
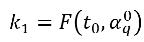
equazione 2.153
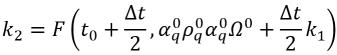
equazione 2.154
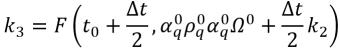
equazione 2.155
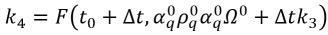
equazione 2.156
Per il sistema a n fasi, in genere vengono risolte solo frazioni di volume di fase (n-1) e quella rimanente viene ottenuta dal vincolo fisico, l'equazione 2.142. Tuttavia, potete risolvere tutte le n equazioni di frazione di volume di fase e l'equazione 2.142 viene soddisfatta scalando ciascuna fase utilizzando la somma della frazione di volume totale calcolata. Il risultato può essere minore o più maggiore di 1 in un processo iterativo.