Modelli euleriani e equazioni governanti
In questa sezione vengono descritte le equazioni governanti per i modelli multifase VOF e di miscela, la modellazione della turbolenza e i limiti nei flussi multifase.
Equazioni governanti multifase generali
Nell'approccio Euler-Euler, si presume che le diverse fasi o i componenti di un sistema multifase siano continui matematicamente che condividono la stessa pressione di flusso. Poiché lo spazio fisico o il volume sono condivisi da tutte le fasi, viene introdotto il concetto di frazione di volume di fase per descrivere il trasporto di fase. Si assume inoltre che le frazioni del volume di fase siano funzioni continue di spazio e tempo e che la loro somma sia uguale a uno. Le leggi di conservazione sono applicate per ogni fase in modo da derivare un insieme di equazioni governanti, che sono chiuse da relazioni costitutive teoriche o empiriche. Nell'approccio Euler-Euler esistono due tipi di modelli utilizzati regolarmente:
• Modello multifluido non omogeneo o euleriano - Risolve direttamente le equazioni governanti in ogni fase, compresa la fase di equazioni di momento, energia, turbolenza, specie e frazione di volume. Le interazioni fase-fase e i trasferimenti interfase di momento, massa, specie e calore sono modellati da sotto-modelli fisici.
Utilizzando lo scalare di fase generale, ϕq, q per la fase qth, l'equazione generalizzata per la fase q ha la seguente forma:
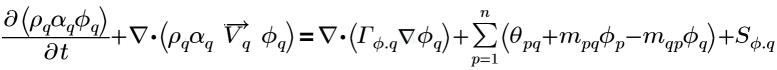
equazione 2.54
dove
ρq | densità q |
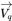 | velocità |
Sϕq | termine origine |
Tϕq | coefficiente di diffusione |
αq | frazione di volume nella q-esima fase |
e ϕq rappresenta le variabili dipendenti in un sistema multifase:
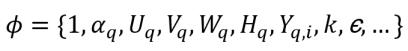
equazione 2.55
dove
Uq, Vq, Wq | componenti della velocità di fase |
Hq | entalpia totale della fase |
Yqi | frazione di massa delle specie "i" nella q-esima fase |
k | Energia cinetica turbolenta |
ε | tasso di dissipazione dell'energia cinetica turbolenta per i modelli k-ε |
Nell'equazione 2.54 il secondo termine sul lato destro rappresenta gli scambi interfase. In particolare,
p | p-esima fase |
n | numero di fasi nel sistema multifase |
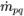 | trasferimento di massa dalla q-esima fase alla p-esima fase |
θpq | scambio diretto di fase delle quantità di trasporto tra cui momento, energia e specie |
Utilizzando i sottomodelli per le specie interfase, la massa, il momento e gli scambi di calore, è possibile derivare l'insieme completo di equazioni che governano il flusso dalle equazioni di trasporto qui generalizzate.
• Modello multifase omogeneo - Alternativa semplificata ed economica al modello disomogeneo. L'approccio di modellazione omogeneo calcola in media la fase che governa le equazioni di flusso, energia e turbolenza per ottenere un insieme di equazioni di trasporto della miscela, mentre le frazioni del volume di fase sono ancora risolte. Per lo scalare della miscela, ϕm, l'equazione governante generalizzata ha la seguente espressione:
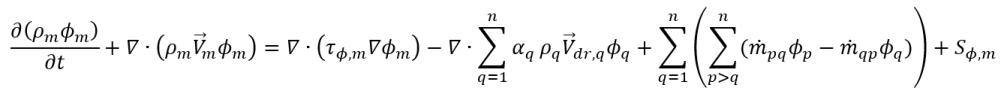
equazione 2.56
dove
m | miscela di fasi |
tutte le variabili con m | valori medi di miscela o fase |
e 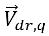 è la differenza tra la velocità della fase q e la velocità della miscela:
è la differenza tra la velocità della fase q e la velocità della miscela:
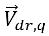 è la differenza tra la velocità della fase q e la velocità della miscela:
è la differenza tra la velocità della fase q e la velocità della miscela: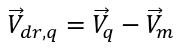
Il modello multifase omogeneo è un caso limite del flusso multifase Euler-Euler in cui la velocità di trasferimento interfase è elevata. Il presupposto fondamentale è che tutte le fasi condividano lo stesso campo di pressione. Con questa ipotesi, il modello omogeneo porta all'ulteriore semplificazione del modello multifluido euleriano disomogeneo completo assumendo che tutte le fasi condividano una velocità, una temperatura e un campo di turbolenza comune. Questo approccio è un valido sostituto del modello multifluido euleriano completo grazie alla sua facile implementazione e all'economia computazionale. Fisicamente, senza il requisito di modelli di scambio interfase nelle equazioni di quantità di momento ed energia, il modello omogeneo può eseguire sia il modello multifluido completo in casi come flussi superficiali liberi (VOF), cavitazione o altri flussi multifase altamente miscelati.
In Creo Flow Analysis, il modulo multifase corrente adotta solo l'approccio di modellazione omogeneo. L'attenzione è focalizzata sulla modellazione del flusso superficiale libero (modello di volume di fluido) e dei flussi omogenei a due fasi liquido-gas (modello di miscela). In linea di principio, potete applicare la capacità di modellazione per flussi a n fasi.
Modelli multifase VOF e di miscela
I modelli multifase VOF e di miscela utilizzano l'approccio di modellazione omogeneo. L'equazione di trasporto della frazione di volume ad ogni fase viene ottenuta dall'equazione 2.54. Le equazioni governanti per lo slancio e l'energia di miscela sono derivate tramite l'equazione 2.56 e le leggi di conservazione della massa, di momento e di energia. In questa sezione è riportato l'insieme delle equazioni governanti.
• Equazione di frazione di volume a q fasi
Nell'equazione 2.54, impostando ϕq=1, si ottiene l'equazione della frazione di volume della fase q:
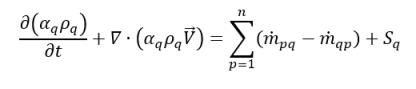
equazione 2.57
dove il tasso di termini di scambio di massa 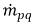 e
e 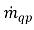 rappresentano la grandezza di origine e risucchio rispettivamente per la fase q. In un processo di trasferimento di massa interfase, uno dei due termini di solito è zero. Considerate l'esempio seguente:
rappresentano la grandezza di origine e risucchio rispettivamente per la fase q. In un processo di trasferimento di massa interfase, uno dei due termini di solito è zero. Considerate l'esempio seguente:
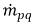 e
e 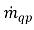 rappresentano la grandezza di origine e risucchio rispettivamente per la fase q. In un processo di trasferimento di massa interfase, uno dei due termini di solito è zero. Considerate l'esempio seguente:
rappresentano la grandezza di origine e risucchio rispettivamente per la fase q. In un processo di trasferimento di massa interfase, uno dei due termini di solito è zero. Considerate l'esempio seguente:In un processo di evaporazione, la fase q liquida perde massa, 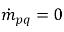 e
e 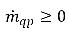 , mentre in fase di vapore
, mentre in fase di vapore 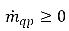 e
e 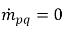 .
.
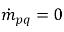 e
e 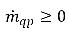 , mentre in fase di vapore
, mentre in fase di vapore 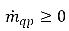 e
e 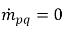 .
.Per un sistema a n fasi, la somma delle frazioni di volume di fase soddisfa il vincolo fisico:
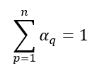
equazione 2.58
O la conservazione della massa totale:
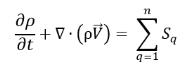
equazione 2.59
dove le quantità di miscela vengono definite di seguito:
◦ Densità della miscela mediata sul volume
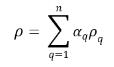
equazione 2.60
◦ Velocità della miscela mediata sulla massa
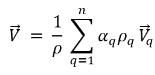
equazione 2.61
• Equazione del momento per la miscela - Ottenuta sommando le singole equazioni di momento per tutte le fasi nel sistema. Dall'equazione 2.56 impostando 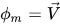 , si ha
, si ha
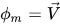 , si ha
, si ha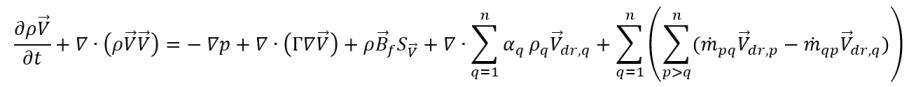
equazione 2.62
dove le quantità di miscela vengono definite di seguito.
◦ Viscosità della miscela mediata sul volume:

equazione 2.63
Il coefficiente di diffusione Γ nell'equazione 2.62 viene calcolato utilizzando la viscosità dinamica della miscela μ e la viscosità turbolenta μt. Gli ultimi due termini sul lato destro rappresentano il trasferimento del momento diretto e lo scambio del momento indotto dal trasferimento di massa. Questi sono determinati dalle velocità di deriva delle fasi, 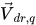 definite come:
definite come:
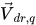 definite come:
definite come:
equazione 2.69
Nell'approccio omogeneo, potete modellare questa velocità di deriva utilizzando un modello algebrico. Tuttavia, nel modello VOF e di miscela corrente, non si assume alcuno slittamento tra le fasi:
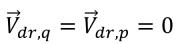
Di conseguenza, entrambi termini di scambio del momento sono uguali a zero.
◦ Equazione di energia della miscela
Senza lo slittamento della velocità, l'equazione di energia per la miscela ha la seguente forma:
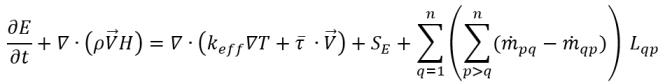
equazione 2.70
dove le variabili della miscela vengono definite di seguito.
▪ Conduttività termica mediata sul volume
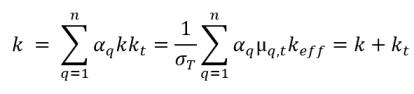
equazione 2.71
▪ Energia ed entalpia della miscela mediate sulla massa
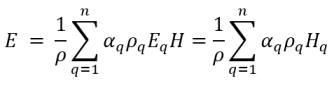
equazione 2.72
Nell'equazione 2.70 dell'energia della miscela, il termine di riscaldamento viscoso 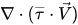 viene calcolato come flusso monofase ed SE è l'origine di calore utente o esterno totale.
viene calcolato come flusso monofase ed SE è l'origine di calore utente o esterno totale.
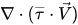 viene calcolato come flusso monofase ed SE è l'origine di calore utente o esterno totale.
viene calcolato come flusso monofase ed SE è l'origine di calore utente o esterno totale.L'ultimo termine sul lato destro è il trasferimento di calore dell'interfaccia causato dal trasferimento di massa. Assumendo che le fasi condividano la stessa temperatura, Lgp dipende dalla definizione di Hq e Hp nell'equazione di energia risolta.
Come descritto nel modulo Calore (Heat), l'entalpia statica di un materiale è costituita da due parti: entalpia di riferimento dello stato standard ed entalpia sensibile. Presupponendo che la fase q e la fase p siano rispettivamente liquido e vapore, allora l'entalpia statica totale di fase sarà:
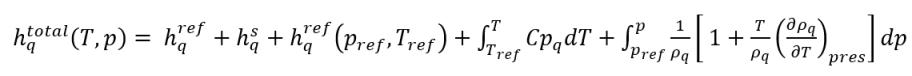
equazione 2.73
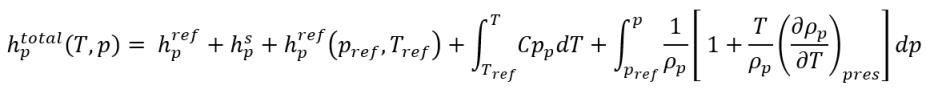
equazione 2.74
dove
pref | pressione di riferimento |
Tref | temperatura di riferimento |
hq,ref | entalpie di riferimento dello stato standard fase-q |
hp,ref | entalpie di riferimento dello stato standard fase-p |
La differenza delle entalpie di riferimento
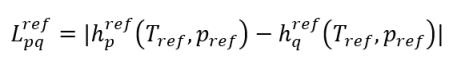
equazione 2.75
è il calore latente alla temperatura Tref e alla pressione pref di riferimento.
▪ Inclusione dell'entalpia di riferimento standard
Nell'equazione 2.70, se l'entalpia H è l'entalpia totale della miscela, si ha
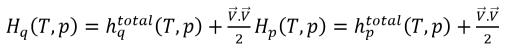
equazione 2.76
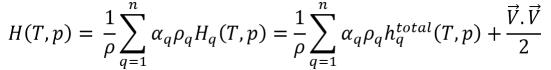
equazione 2.77
Quindi la differenza dovuta alle entalpie di formazione delle fasi o al calore latente Lpq è già stata inclusa nell'equazione di energia. La quantità è impostata su zero:
Lpq=0
E il trasferimento di calore a causa del trasferimento di massa, l'ultimo termine a destra nell'equazione 2.70, è zero nell'equazione di energia della miscela.
▪ Esclusione dell'entalpia di riferimento standard
In un solutore CFD, l'entalpia totale non viene risolta direttamente. Solo l'entalpia sensibile relativa alla temperatura di saturazione è inclusa nell'entalpia risolta e nell'energia interna:
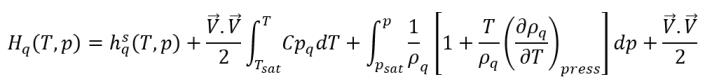
equazione 2.79
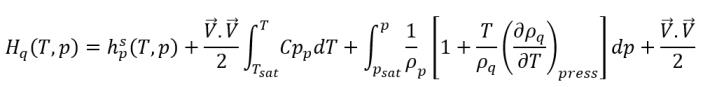
equazione 2.80
Quindi Lpq non è zero. Deve essere il calore latente:
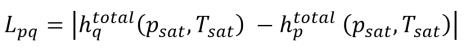
equazione 2.81
dove
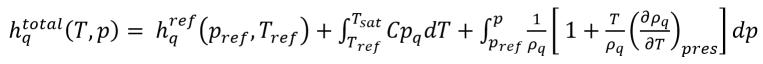
equazione 2.82
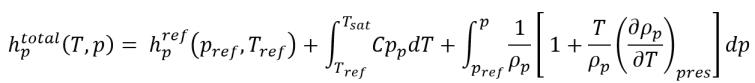
equazione 2.83
In Creo Flow Analysis, per default, l'entalpia di riferimento dello stato standard viene considerata automaticamente. Non è necessario alcun input dell'utente.
Modelli di turbolenza
• Modelli di turbolenza k-ε della miscela
Nei modelli multifase VOF e di miscela, l'effetto della turbolenza sulla miscela delle fasi è tenuta in considerazione utilizzando le estensioni dei modelli di turbolenza monofase. I modelli di turbolenza e i trattamenti in prossimità della parete, descritti nel modulo Turbolenza (Turbulence), vengono estesi ai flussi multifase in Creo Flow Analysis. Con le quantità del flusso di miscela, i modelli standard e k-ε RNG hanno le stesse forme generali dei modelli di turbolenza monofase:
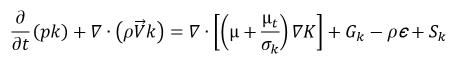
equazione 2.84
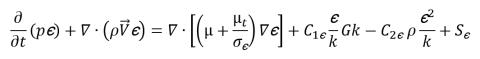
equazione 2.85
dove la densità della miscela ρ, la velocità 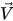 e la viscosità molecolare μ sono calcolate dai rispettivi valori di fase utilizzando le relazioni nell'equazione 2.60, nell'equazione 2.61 e nell'equazione 2.63; Sk e Sε includono entrambe le possibili sorgenti esterne e dell'utente e le sorgenti di interazione di fase. La viscosità turbolenta per la miscela, μt viene calcolata direttamente da un'espressione:
e la viscosità molecolare μ sono calcolate dai rispettivi valori di fase utilizzando le relazioni nell'equazione 2.60, nell'equazione 2.61 e nell'equazione 2.63; Sk e Sε includono entrambe le possibili sorgenti esterne e dell'utente e le sorgenti di interazione di fase. La viscosità turbolenta per la miscela, μt viene calcolata direttamente da un'espressione:
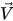 e la viscosità molecolare μ sono calcolate dai rispettivi valori di fase utilizzando le relazioni nell'equazione 2.60, nell'equazione 2.61 e nell'equazione 2.63; Sk e Sε includono entrambe le possibili sorgenti esterne e dell'utente e le sorgenti di interazione di fase. La viscosità turbolenta per la miscela, μt viene calcolata direttamente da un'espressione:
e la viscosità molecolare μ sono calcolate dai rispettivi valori di fase utilizzando le relazioni nell'equazione 2.60, nell'equazione 2.61 e nell'equazione 2.63; Sk e Sε includono entrambe le possibili sorgenti esterne e dell'utente e le sorgenti di interazione di fase. La viscosità turbolenta per la miscela, μt viene calcolata direttamente da un'espressione: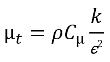
equazione 2.86
durante la produzione di energia cinetica turbolenta viene calcolata in base ai gradienti di velocità e viscosità turbolenta:
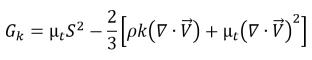
equazione 2.87
dove S è il modulo del tasso di deformazione medio della miscela, 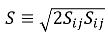
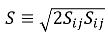
La viscosità turbolenta per la fase-q può essere calcolato come:
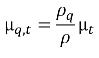
equazione 2.87
• Effetto della diffusione turbolenta
Per i flussi turbolenti multifase, una forza di dispersione turbolenta sorge quando si media il termine di resistenza interfacciale istantaneo, che si comporta come quello della diffusione di fase. Il modello multifluido euleriano non omogeneo tratta in genere questo effetto turbolento come forza interfase aggiuntiva, determinata da gradienti di frazioni di volume di fase nelle equazioni di momento di fase. Tuttavia, questo effetto turbolento può essere modellato direttamente considerandolo come termine di diffusione turbolenta nelle equazioni di frazioni di volume di fase. Dividendo 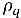 e raggruppando tutte le sorgenti come
e raggruppando tutte le sorgenti come 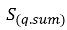 (la somma delle origini di massa di trasferimento interfase ed esterne), avrete la seguente equazione governante per la frazione di volume della fase-q nei flussi turbolenti:
(la somma delle origini di massa di trasferimento interfase ed esterne), avrete la seguente equazione governante per la frazione di volume della fase-q nei flussi turbolenti:
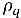 e raggruppando tutte le sorgenti come
e raggruppando tutte le sorgenti come 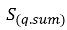 (la somma delle origini di massa di trasferimento interfase ed esterne), avrete la seguente equazione governante per la frazione di volume della fase-q nei flussi turbolenti:
(la somma delle origini di massa di trasferimento interfase ed esterne), avrete la seguente equazione governante per la frazione di volume della fase-q nei flussi turbolenti: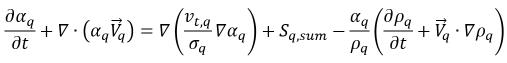
dove il primo termine sulla destra è il termine di diffusione turbolenta nella fase-q, che deve soddisfare il vincolo riportato di seguito in modo che la massa totale sia conservata:
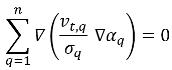
I termini di diffusione turbolenta di solito sono implementati come opzione. Per default, questa opzione non è inclusa.
Modellazione dei limiti multifase
Nei modelli multifase VOF e di miscela, le condizioni al limite per le equazioni di flusso e di energia sono uguali a quelle nei flussi monofase. Tali condizioni sono descritte nei moduli Flusso (Flow) e Calore (Heat). Per frazioni di volumi di fase, di seguito vengono applicati solo valori fissi e gradienti zero.
• Limite di ingresso per n fasi
Per (n-1) fasi, le frazioni di volumi in ingresso sono predeterminate, mentre la n-esima fase viene ottenuta mediante il vincolo fisico:
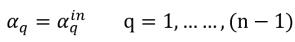
equazione 2.88
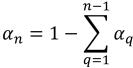
equazione 2.89
La frazione di volume per ogni fase deve essere non negativa.
• Limite di uscita/simmetria/parete
Per (n-1) fasi, le condizioni a gradiente zero si applicano a tutti i limiti di uscita, simmetria e pareti, mentre la n-esima fase viene ottenuta mediante il vincolo fisico:
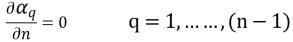
equazione 2.90
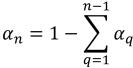
equazione 2.91
Le equazioni governanti precedenti, i modelli di turbolenza e le condizioni al limite rappresentano la base dei modelli multifase VOF e di miscela omogenei. Senza funzioni sorgente esterne o definite dall'utente e trasferimenti di massa interfase, queste equazioni sono un sistema chiuso di equazioni e vengono risolte numericamente utilizzando un solutore multifase a volume finito basato sulla pressione. Numerose applicazioni pratiche, alcuni sotto-modelli specifici come la forza di tensione superficiale nei modelli VOF e i trasferimenti di massa interfase, sono essenziali per acquisire i rispettivi processi e fenomeni fisici in maniera accurata. Invece di ridurre i sottomodelli a sorgenti esterne o utente, è preferibile includerli direttamente nei modelli integrati.