Kavitationsmodelle
In Creo Flow Analysis wird die Arbeitsflüssigkeit in Kavitationsflüssen ebenso wie im ursprünglichen Modell von Singhal et al als eine Mischung aus Flüssigkeit, Dampf und nicht kondensierbaren Gasen betrachtet. Standardmäßig berücksichtigen die Kavitationsmodelle sowohl den Phasenübergang von Flüssigkeit zu Dampf als auch den Effekt von nicht kondensierbaren Gasen. Basierend auf den Modellierungsansatz für den Effekt nicht kondensierbarer Gase werden fünf verschiedene Modelle in der folgenden Tabelle bereitgestellt, um die Belüftung und Kavitation in einem Flüssigkeitssystem vorherzusagen. Diese Modelle werden in diesem Abschnitt ausführlich beschrieben.
|
Modelle für NKG
|
Beschreibung
|
|---|---|
|
Konstanter Gasmassenanteil
|
Der Massenanteil von nicht kondensierbarem Gas (NKG) ist konstant und wird als außerhalb der Lösung mit sehr kleinen kompressiblen Blasen betrachtet.
|
|
Variabler Gasmassenanteil
|
Ähnlich wie das konstante Gasmassenanteilmodell, jedoch kann der Massenanteil von NKG variieren; beispielsweise können Zuflüsse zu unterschiedlichen Massenanteilen führen.
|
|
Gleichgewichtig gelöstes Gasmodell
|
Der Massenanteil des in der Flüssigkeit gelösten NKG entspricht dem Gleichgewichtswert.
|
|
Gelöstes Gasmodell
|
Der Massenanteil des in der Flüssigkeit gelösten NKG hängt von der Absorptions- oder Desorptionsrate und dem Gleichgewichtswert ab
|
|
Vollständiges Gasmodell
|
Kombiniert das gelöste Gasmodell und den variablen Gasmassenanteil
|
Konstantes Gasmassenanteilmodell
Das Modell des konstanten Gasmassenanteils ist das grundlegende oder Standard-Kavitationsmodell in Creo Flow Analysis. Es basiert auf der Arbeit von Singhal et al. Dieses Modell geht davon aus, dass das stets vorhandene nicht kondensierbare Gas (NKG) in der Arbeitsflüssigkeit ein nicht lösliches Gas ist bzw. freien Gasblasen sind, die der allgemeinen Gasgleichung folgen. Obwohl das gesamte vorgegebene nicht kondensierbare Gas mit der Abnahme des Drucks in Kavitationszonen frei expandieren kann, ist der Massenanteil nicht kondensierbarer Gase vorgegeben und bleibt in einem Kavitationsfluss unverändert:
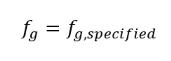
Gleichung 2.217
Hierbei ist fg,specified ein vom Benutzer angegebener Wert.
Die Dichte des nicht kondensierbaren Gases folgt der allgemeinen Gasgleichung:
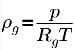
Gleichung 2.218
wobei T die Temperatur der Flüssigkeit ist, die vorgegeben ist (isothermischer Fluss) oder durch Lösen der Gleichung 2.168 der Mischungsenergieerhaltung ermittelt wird, wenn eine Wärmeübertragung berücksichtigt wird. Aus Gleichung 2.173 ist der Volumenanteil des nicht kondensierbaren Gases wie folgt:
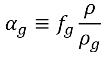
Gleichung 2.219
Obwohl der Massenanteil von NKG fest ist und normalerweise in Naturwasser einen sehr kleinen Wert von 1,5e-05 oder 15 ppm hat, variiert sein Volumenanteil αg deutlich und kann einen höheren Wert haben. In Kavitäten oder Niederdruckzonen konkurriert das nicht kondensierbare Gas mit dem Dampf, um den Leerraum zu füllen, abhängig von den Gas- und Dampfdichten.
Für den Flüssigkeit-Dampf-Massenübergang dienen Gleichung 2.194 und Gleichung 2.195 als Grundlage zum Erstellen des Quellen- und Senken-Terms der Kavitation in der Dampfmassenanteilgleichung, der Gleichung 2.169. Insbesondere muss der Blasenradius RB mit den bekannten Flussmengen während des Blasenwachstums und des Blasenzusammenbruchs geschätzt werden. Singhal et al argumentierte, dass dann, wenn die typische Blasengröße RB mit der (maximal möglichen) Grenz-Blasengröße identisch ist, RB durch das Gleichgewicht zwischen den aerodynamischen Zug- und Oberflächenspannungskräften bestimmt wird. In der Atomindustrie wird die folgende Korrelation verwendet:
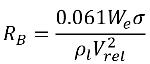
Gleichung 2.220
wobei Vrel der Betrag der relativen Flüssigkeit-Dampf-Geschwindigkeit ist. Im Blasenströmungsmodell (in dem Kavitation auftritt), ist Vrel im Allgemeinen klein und beträgt um die 5 bis 10 % der Flüssigkeitsgeschwindigkeit. Durch Verwendung verschiedener einschränkender Argumente wie RB →0 als αv →0 und der Tatsache, dass die Phasenübergangsraten pro Volumeneinheit proportional zu den Volumenanteilen (oder Massenanteilen) der Spenderphase sein sollten, werden folgende Begriffe für Dampferzeugungs/-kondensationsraten ermittelt, um das Kavitationsmodell wie folgt fertig zu stellen:
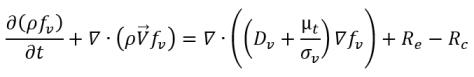
Gleichung 2.221
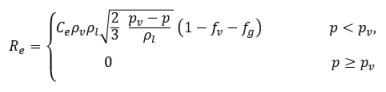
Gleichung 2.222
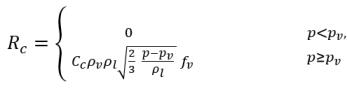
Gleichung 2.223
Hierbei sind Ce und Cc die Verdampfungs- und Kondensationskoeffizienten, die vom Benutzer angegebene konstante Werte, die standardmäßig auf 1.0 festgelegt sind, oder Funktionen von bekannten Flussmengen sein können. In Gleichung 2.222 und Gleichung 2.223 wird ein neuer Schwellenwertdruck ρv eingeführt, um den Sättigungsdampfdruck ρsat in Gleichung 2.194 und Gleichung 2.195 zu ersetzen. Gemäß Singhal et al wird zur Berücksichtigung des Effekts der Turbulenz auf Kavitationsflüsse, beobachtet durch experimentelle Untersuchungen, ein lokaler Wert der turbulenten Druckschwankungen verwendet, angegeben durch Hinze:
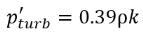
Gleichung 2.224
dem Sättigungsdampfdruck hinzugefügt, um den Schwellenwertdruck für den Phasenübergang zu erhöhen:
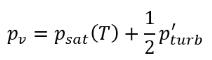
Gleichung 2.225
Für laminare Flüsse: pv=psat(T)
Wenn Wärmeübertragung berücksichtigt wird und alle Phasendichten einschließlich Flüssigkeit, Dampf und nicht kondensierbare Gase Temperaturänderungen unterliegen, ist der Sättigungsdampfdruck psat auch eine Funktion der Temperatur. Daher kann der direkte thermische Effekt auf die Kavitation in diesem Kavitationsmodell berücksichtigt werden.
Variables Gasmassenanteilmodell
Beim variablen Gasmassenanteilmodell wird angenommen, dass das nicht kondensierbare Gas immer ein freies Gas bleibt, das nicht in der Flüssigkeit gelöst werden kann, aber der Massenanteil ist keine vorgegebene Konstante mehr wie im konstanten Gasmassenanteilmodell. Stattdessen wird die Verteilung des lokalen Massenanteils durch eine Transportgleichung vorgegeben. Während der Massenübergang von Flüssigkeit zu Dampf durch das gleiche Kavitationsmodell modelliert wird, das in Gleichung 2.221, Gleichung 2.222 und Gleichung 2.223 referenziert wird. Aus Gründen der Übersichtlichkeit ist nachstehend der vollständige Satz der Modellierungsgleichungen angegeben:
• Phasenübergang Flüssigkeit-Dampf
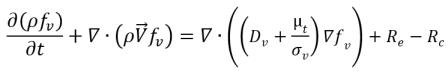
Gleichung 2.226
Dabei gilt:
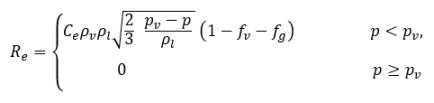
Gleichung 2.227
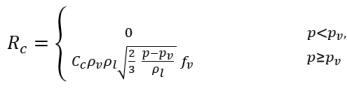
Gleichung 2.228
• Transportgleichung für nicht kondensierbares Gas
Nach Gleichung 2.199 lautet die Transportgleichung für das nicht kondensierbare Gas (fg):
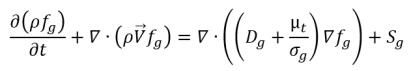
Gleichung 2.229
Hierbei ist Sg die externe oder benutzerdefinierte Quelle für das nicht kondensierbare Gas.
Gleichgewichtig gelöstes Gasmodell
In Kavitationsflüssen werden die nicht kondensierbaren Gase in der Flüssigkeit in eine Flüssigkeit gelöst oder aus einer solchen freigesetzt, um ein dynamisches Gleichgewicht der Massenkonzentrationen zwischen der flüssigen und gasförmigen Phase zu erzielen. Im gleichgewichtig gelösten Gasmodell wird angenommen, dass der Massenanteil des nicht kondensierbaren Gases konstant bleibt. Ein Teil davon wird jedoch in die Flüssigkeit gelöst, um die lokale Gleichgewichtsbedingung sofort zu erfüllen. Mathematisch löst es zusätzlich zu der gleichen Massenanteilsgleichung für Dampf und Dampf-Massenübergangsmodellen eine zusätzliche Transportgleichung für den Massenanteil des gelösten Gases fgd, der als stets im Gleichgewicht befindlich vorausgesetzt wird. Die Modellierungsgleichungen sind wie folgt:
• Phasenübergang Flüssigkeit-Dampf
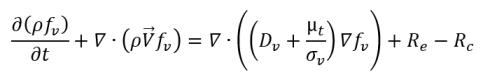
Gleichung 2.230
Dabei gilt:
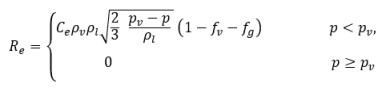
Gleichung 2.231
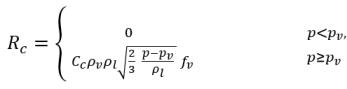
Gleichung 2.232
• Gasabsorption/-lösung oder -freisetzung
Aus Gleichung 2.197, Gleichung 2.211 und Gleichung 2.212 hat die Gleichung für den Transport von gelöstem Gas folgende Form:
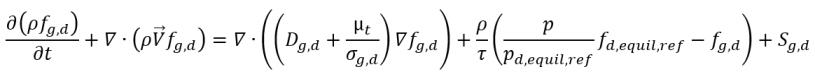
Gleichung 2.233
Dabei gilt:
Sg,d | benutzerdefiniertes Gesetz der Gaslösung oder -freisetzung |
fd,equil,ref | Gleichgewichtsmassenanteil des gelösten Gases beim Referenzdruck pd,equil,ref |
fd,equil,ref und pd,equil,ref | Vom Benutzer festgelegte Werte |
In diesem Gleichgewichtsmodell nähert sich die Zeitskala Γ null, sodass der Massenübergang nahezu sofort erfolgt. Beachten Sie, dass in Gleichung 2.231 das freie Gas den Massenanteil fg,f statt fg hat. Der Massenanteil des freien Gases wird aus der folgenden Bedingung ermittelt:
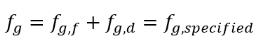
Gleichung 2.234
Hierbei ist fg,specified ein vom Benutzer angegebener Wert.
Gelöstes Gasmodell
Dieses Modell lockert die Bedingung, dass sich das gelöste Gas in der Flüssigkeit immer im Gleichgewichtszustand befindet. Statt als Gleichgewichtsbedingung mit sofortigem Massenübergang bestimmt zu werden, hängt der Massenanteil des gelösten Gases (fg,d) vom Transport der Komponente und der Lösungs- oder Freisetzungsrate (finite Rate) ab. Daher werden für das gelöste Gasmodell dieselben Modellierungsformeln wie für das gleichgewichtig gelöste Gasmodell verwendet, Gleichung 2.230 bis Gleichung 2.234. Die finiten Raten des Massenübergangs für die Gaslösung und -freisetzung sind durch verschiedenen Zeitskalen (Γ) gekennzeichnet. Für die Gasabsorption oder -lösung in der Flüssigkeit ist Γ durch eine angegebene Absorptionszeit gegeben (die Lösungszeit von gelöstem Gas ist standardmäßig 10 s). Für die Freisetzung von gelöstem Gas aus der Flüssigkeit ist die Massenübergangsrate durch eine angegebene Gasfreisetzungszeit vorgegeben (der Standardwert t für die Freisetzungszeit von gelöstem Gas Γ ist 10 s).
Vollständiges Gasmodell
Das vollständige Gasmodell ist eine Kombination des gelösten Gasmodells und des variablen Gasmodells. Der Massenanteil des nicht kondensierbaren Gases unterliegt zeitlichen und räumlichen Änderungen, während die Gaslösung oder -absorption und -freisetzung auch bei nicht kondensierbaren Gase auftreten kann. Der vollständige Satz der Modellierungsgleichungen ist nachstehend aufgeführt:
• Phasenübergang Flüssigkeit-Dampf
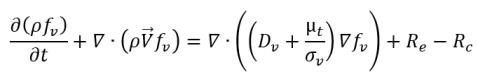
Gleichung 2.235
Dabei gilt:
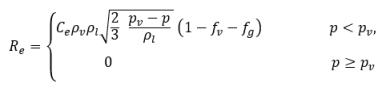
Gleichung 2.236
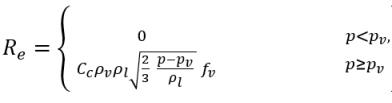
Gleichung 2.237
• Transport von nicht kondensierbarem Gas
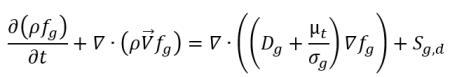
Gleichung 2.238
• Gaslösung oder -freisetzung
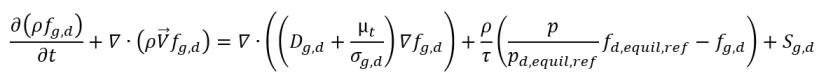
Gleichung 2.239