Theorie der Kavitationsmodelle
In der Gleichung 2.169 für den Dampftransport sind Re und Rc die Quellen-Terme für den Massenübergang, die mit dem Wachstum und Zusammenbruch der Dampfblasen in Kavitationsflüssen verbunden sind. Diese Terme berücksichtigen den Massenaustausch zwischen der Dampf- und der Flüssigphase während eines Kavitationsprozesses. Re und Rc werden auf der Basis der Rayleigh-Plesset-Gleichung modelliert, die das Wachstum einer einzigen Dampfblase in einer Flüssigkeit beschreibt.
Flüssigkeit-Dampf-Massenübergang
Um einen Ausdruck der resultierenden Phasenänderungsrate in der Kavitation abzuleiten, betrachten Sie einen inkompressiblen Flüssigkeit-Dampf-Zweiphasenfluss mit einer Schlupfgeschwindigkeit null, bei dem nicht kondensierbares Gas nicht berücksichtigt wird. Wenn Sie R einführen, um die resultierende Rate des Massenübergangs von der Flüssigkeit zum Dampf darzustellen, lauten die Flüssigkeits- und Dampfvolumengleichungen und die Kontinuitätsgleichung der Gesamtmasse wie folgt:
• Flüssigphase
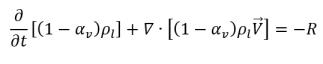
Gleichung 2.179
• Dampfphase
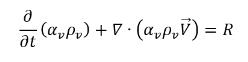
Gleichung 2.180
• Mischung (Gesamtmasse-Kontinuität)
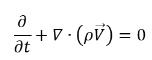
Gleichung 2.181
In dem Flüssigkeit-Dampf-Zweiphasensystem wird die Mischungsdichte ρ als Dampfvolumenanteil und Phasendichten ausgedrückt:
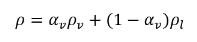
Gleichung 2.182
Da die Flüssigkeits- und die Dampfdichte als konstant (inkompressibel) angenommen werden, wird eine Beziehung zwischen dem Geschwindigkeitsgradienten und dem Dampfvolumenanteil aus Gleichung 2.181 und Gleichung 2.182 abgeleitet:
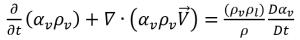
Gleichung 2.183
Durch das Kombinieren von Gleichung 2.179 und Gleichung 2.183 ergibt sich der Ausdruck für den Nettomassenquellen-Term wie folgt:
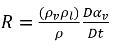
Gleichung 2.184
Durch Substitution der Gleichung 2.184 in Gleichung 2.180 wird die Gleichung für den Dampfvolumenanteil in die allgemeine Form umgeschrieben:
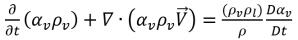
Gleichung 2.185
Durch Anwenden der Beziehung zwischen dem Massenanteil und dem Volumenanteil der Gleichung 2.173 für Dampf erhalten Sie Gleichung 2.185 als Dampfmassenanteil:

Gleichung 2.186
Aus Gleichung 2.185 und Gleichung 2.186 wird klar, dass unter der Bedingung einer Schlupfgeschwindigkeit null zwischen der Flüssigkeits- und der Dampfphase die Kavitation als einphasiger Fluss mit einer zusätzlichen Dampfmassenanteilübergangsgleichung oder als Eulerscher Mehrphasenmischungsfluss mit einem Flüssigkeit-Dampf-Massenübergang modelliert werden kann. Ohne Berücksichtigung des Effekts der Differenz der Diffusions- und Phasengeschwindigkeit sind die zwei Ansätze mathematisch identisch. Creo Flow Analysis verwendet den einphasigen Ansatz zur Modellierung von Kavitationsflüssen.
Hinweise zur Blasendynamik
Bei den meisten natürlichen Vorkommen und technischen Systemen gibt es eine ausreichende Anzahl von Kernen wie Blasen, nicht kondensierbaren Gasen usw. in der Flüssigkeit, um eine Kavitation entstehen zu lassen. Bei der Modellierung des Kavitationsprozesses liegt der Schwerpunkt daher primär auf der korrekten Berücksichtigung von Blasenwachstum und -zusammenbruch. Unter der Annahme, dass in einer fließenden Flüssigkeit eine Schlupfgeschwindigkeit null zwischen der Flüssigkeit und den Dampfblasen besteht, wird die Gleichung der Blasendynamik aus der allgemeinen Rayleigh-Plesset-Gleichung abgeleitet, die das Wachstum einer Gasblase in einer Flüssigkeit beschreibt:
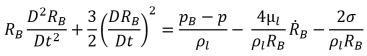
Gleichung 2.187
Dabei gilt:
RB | Blasenradius |
pB | Druck in der Blase (angenommen als der Dampfdruck bei der Flüssigkeitstemperatur bei Fehlen anderer Gase) |
p | Druck in der die Blase umgebenden Flüssigkeit |
σ | Oberflächenspannungskoeffizient zwischen der Flüssigkeit und dem Dampf |
Diese Gleichung wird aus dem mechanischen Gleichgewicht abgeleitet (keine thermischen Barrieren für das Blasenwachstum).
Wenn Sie die quadratische Zeitableitung (geeignet für niederfrequente Schwingung), den viskosen Dämpfungsterm und die Oberflächenspannungskraft vernachlässigen, erhalten Sie einen verkürzten Ausdruck der Gleichung 2.187, der für den asymptotischen Zustand gilt:
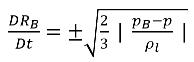
Gleichung 2.188
Diese verkürzte Rayleigh-Plesset-Gleichung liefert einen physikalischen Ansatz, um die Effekte der Blasendynamik in Kavitationsmodelle einzuführen. Der Blasenradius kann je nach den Vorzeichen von (pB–p) zu- oder abnehmen: Die Blase wächst, wenn p<pB, und bricht zusammen, wenn p>pB. Daher wird die Gleichung 2.188 wie folgt umgeschrieben:
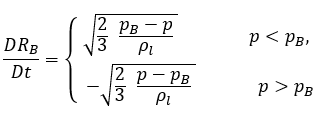
Gleichung 2.189
Wenn η die Dichte der Dampfblasenanzahl in einer Flüssigkeit (die Anzahl der pro Volumeneinheit vorhandenen Blasen) ist und alle Dampfblasen perfekte Kugeln mit demselben Radius RB sind, ist der Dampfphasenvolumenanteil wie folgt:
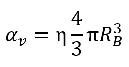
Gleichung 2.190
Es wird angenommen, dass die Dampfblasen in einer Flüssigkeit nicht erzeugt oder zerstört werden können, aber dass die Blasen während eines Kavitationsprozesses wachsen (Verdampfung) und zusammenbrechen (Kondensation) können. In Gleichung 2.190 bleibt die Dampfblasenanzahl-Dichte (η) eine Konstante, während der Blasenradius (RB) zu- oder abnimmt. Dann wird die Zeitableitung des Dampfvolumenanteils wie folgt berechnet:
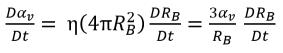
Gleichung 2.191
Wenn man Gleichung 2.191 in Gleichung 2.186 substituiert, erhält man die Transportgleichung für den Dampfphasenmassenanteil:
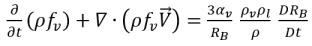
Gleichung 2.192
Durch Anwenden von Gleichung 2.189 ergibt sich für die Nettorate des Massenübergangs pro Volumeneinheit zwischen Flüssigkeit und Dampf die folgende Formel:
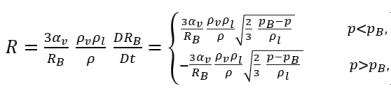
Gleichung 2.193
wobei Gleichung 2.193 angibt, dass bei der Kavitation die Volumeneinheit-Massenübergangsrate (R) die Funktion von (proportional zu) sowohl Dampf- als auch Flüssigphasendichte ist, und auch umgekehrt proportional zur Mischungsdichte ist. Da Gleichung 2.192 direkt aus den Phasen- und Mischungs-Massenkontinuitäten berechnet wird, ist sie exakt und sollte den Massenübergang zwischen der Flüssigkeits- und Dampfphase in der Kavitation genau darstellen. Mit der Einführung der Blasendynamik verwendet Gleichung 2.193 den gleichen Ansatz, um die zwei entgegengesetzten und physikalisch unterschiedlichen Massenübergangsprozesse von Flüssigkeit zu Dampf (Blasenwachstum oder Verdampfung) und von Dampf zu Flüssigkeit (Blasenzusammenbruch oder Kondensation) zu modellieren. Bei der Transportgleichung für den Dampfmassenanteil Gleichung 2.192 ist das Blasenwachstum ein Quellen-Term, während der Blasenzusammenbruch ein Senken-Term ist.
In praktischen Kavitationsmodellen wird normalerweise angenommen, dass der lokale Fernfelddruck p gleich dem Druck in der Zellenmitte ist. Der Blasendruck pB ist gleich dem Sättigungsdampfdruck (psat, eine Materialeigenschaft) bei Fehlen von gelösten Gasen, Massenübergang und viskoser Dämpfung pB=psat
Vergleicht man Gleichung 2.192 und Gleichung 2.193 mit der allgemeinen Gleichung 2.169 für den Dampfmassenanteil, sind die Quellen-Terme Re und Rc wie folgt:
• Wenn der lokale Fließdruck unterhalb des Sättigungsdampfdrucks, p<psat liegt, tritt nur eine Verdampfung auf, sodass Folgendes gilt:
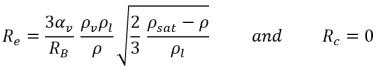
Gleichung 2.194
• Wenn der lokale Fließdruck oberhalb des Sättigungsdampfdrucks, p>psat liegt, tritt nur eine Kondensation auf:
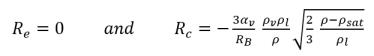
Gleichung 2.195
Gleichung 2.194 und Gleichung 2.195 bilden die Grundlage nahezu aller verfügbaren mechanistischen Zweiphasen-Kavitationsmodelle: Creo Flow Analysis verwendet den Modellierungsansatz von Singhal et. al.
Gasabsorption/-lösung oder -freisetzung
Nicht kondensierbare Gase sind in einer Arbeitsflüssigkeit oft vorhanden und können erhebliche Auswirkungen auf die Kavitation haben. Manchmal wird ein nicht kondensierbares Gas frei mit der Flüssigkeit transportiert und löst sich auch in einer Flüssigkeit oder wird aus einer Flüssigkeit freigesetzt, mit dem Ziel, ein dynamisches Gleichgewicht der Massenkonzentrationen zwischen den Flüssigkeits- und Gasphasen zu erreichen. Die Gasabsorption, -lösung und -freisetzung in einer Flüssigkeit ist ebenfalls ein Phänomen des Flüssigkeit-Dampf-Massenübergangs, das durch die Unterschiede und Gradienten der Massenkonzentration gesteuert wird. Für die Modellierung von Kavitationsflüssen ist es notwendig, auch den Effekt des nicht kondensierbaren Gases und den möglichen Flüssigkeit-Dampf-Massenübergang im Mischungsfluss zu berücksichtigen.
Unter der Annahme, dass in einem Flüssigkeit-Dampf-Zweiphasenfluss ein nicht kondensierbares Gas wie Luft oder Sauerstoff sowohl in der Flüssigphase (gelöstes Gas) als auch in der Gasphase (freies Gas) vorhanden ist, sehen die Gasmassenanteil-Transportgleichungen in jeder Phase wie folgt aus:
• Freies Gas (Gasphase)
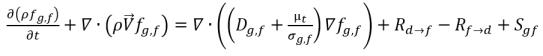
Gleichung 2.196
• Gelöstes Gas (Flüssigphase)
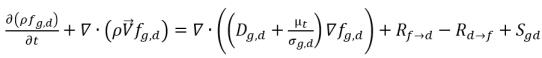
Gleichung 2.197
Dabei gilt:
fg,f | Massenanteile des freien Gases |
fg,d | Massenanteile des freien Gases und des gelösten Gases |
Sg,f, Sg,d | externe oder benutzerdefinierten Quellen |
Dg,f | Diffusität des freien Gases und des gelösten Gases |
Dg,d | Diffusität des gelösten Gases |
Wenn der Massenanteil eines nicht kondensierbaren Gases als fg vorgegeben ist, dann ist:
fg=fg,f
oder sein Transport in Raum und Zeit wird durch Lösen der folgenden Gleichung bestimmt:
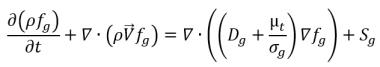
Gleichung 2.199
Beachten Sie, dass für Gleichung 2.196, Gleichung 2.197 und Gleichung 2.199 2.199 nur zwei dieser Gleichungen direkt gelöst werden sollten.
In Gleichung 2.196 und Gleichung 2.197 gibt die Quelle Rd→f die Freisetzungsrate des gelösten Gases und Rf→d die Absorptions- oder Lösungsrate des freien Gases an.
Wenn die zwei Phasen in Kontakt sind, tendieren das freie Gas f und das gelöste Gas d, die aus einer Phase in die andere transportiert werden, dazu, ein dynamisches Gleichgewicht zwischen den zwei Phasen zu erreichen. Die Gleichgewichtsmodelle nehmen an, dass die volumetrischen Raten der Massenübergänge von den Massekonzentrationsgradienten oder -unterschieden abhängen:
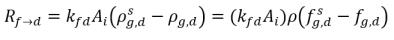
Gleichung 2.200
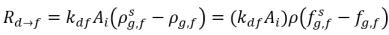
Gleichung 2.201
Dabei gilt:
AI | Flüssigkeit-Gas-Schnittstellenbereich |
kf,d(=kd,f) | Volumetrischer Massenübergangskoeffizient |
ρg,d(=ρfg,d) | lokale Massenkonzentrationen von gelöstem Gas |
ρg,f(=ρfg,f) | lokale Massenkonzentrationen von freiem Gas |
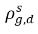 | Gleichgewichtsmassenkonzentrationen des gelösten Gases in seinen Hostingphasen |
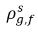 | Gleichgewichtsmassenkonzentrationen des freien Gases in seinen Hostingphasen |
Beachten Sie, dass 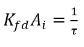 die Einheit der inversen Zeit, 1/s, hat, ein Indikator für Massenübergangseffizienz. Daher haben die Gleichung 2.200 und die Gleichung 2.201 auch die folgenden Formen:
die Einheit der inversen Zeit, 1/s, hat, ein Indikator für Massenübergangseffizienz. Daher haben die Gleichung 2.200 und die Gleichung 2.201 auch die folgenden Formen:
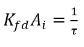 die Einheit der inversen Zeit, 1/s, hat, ein Indikator für Massenübergangseffizienz. Daher haben die Gleichung 2.200 und die Gleichung 2.201 auch die folgenden Formen:
die Einheit der inversen Zeit, 1/s, hat, ein Indikator für Massenübergangseffizienz. Daher haben die Gleichung 2.200 und die Gleichung 2.201 auch die folgenden Formen:
Gleichung 2.202

Gleichung 2.203
In der Regel sind 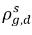 und
und  nicht gleich (Diskontinuität). Es gibt eine optimal definierte Gleichgewichtskurve zwischen den beiden Konzentrationen, die von der Temperatur, vom Druck und von den Mischungszusammensetzungen abhängt. Die Kurve ist normalerweise gleichförmig und nichtlinear und wird häufig als quasilineare Beziehung mit dem Koeffizienten
nicht gleich (Diskontinuität). Es gibt eine optimal definierte Gleichgewichtskurve zwischen den beiden Konzentrationen, die von der Temperatur, vom Druck und von den Mischungszusammensetzungen abhängt. Die Kurve ist normalerweise gleichförmig und nichtlinear und wird häufig als quasilineare Beziehung mit dem Koeffizienten 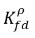 ausgedrückt,
ausgedrückt,
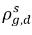 und
und  nicht gleich (Diskontinuität). Es gibt eine optimal definierte Gleichgewichtskurve zwischen den beiden Konzentrationen, die von der Temperatur, vom Druck und von den Mischungszusammensetzungen abhängt. Die Kurve ist normalerweise gleichförmig und nichtlinear und wird häufig als quasilineare Beziehung mit dem Koeffizienten
nicht gleich (Diskontinuität). Es gibt eine optimal definierte Gleichgewichtskurve zwischen den beiden Konzentrationen, die von der Temperatur, vom Druck und von den Mischungszusammensetzungen abhängt. Die Kurve ist normalerweise gleichförmig und nichtlinear und wird häufig als quasilineare Beziehung mit dem Koeffizienten 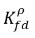 ausgedrückt,
ausgedrückt,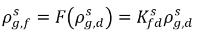
Gleichung 2.204
wobei Kf,d normalerweise mithilfe von physikalischen Gesetze oder empirischen Korrelationen entschieden wird. Ein üblicher Ansatz besteht darin, dem Gesetz von Henry zu folgen, das eine generalisierte Gleichgewichtsbeziehung liefert. Es besagt, dass für eine Flüssigkeitsmischung, die in Kontakt mit der Gasphase ist, der Partialdruck des freien Gas ρg,f gleich dem Produkt des Molenbruchs des gelösten Gases im Gleichgewicht in der Flüssigphase, 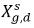 und der Henry-Konstante, Hx, ist:
und der Henry-Konstante, Hx, ist:
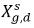 und der Henry-Konstante, Hx, ist:
und der Henry-Konstante, Hx, ist:
Gleichung 2.205
Wenn die freie Gasphase der allgemeinen Gasgleichung folgt, ergibt das Dalton'sche Gesetze des Partialdrucks die folgende Gleichung:
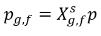
Gleichung 2.206
Unter Verwendung von Gleichung 2.204 – Gleichung 2.206 wird das folgende Gleichgewichtsverhältnis generiert:
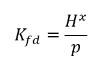
Gleichung 2.207
Daher hat die Henry-Konstante eine Druckeinheit und kann als Referenzdruck betrachtet werden. Angenommen, dass für eine ideale Flüssigkeitsmischung in Kontakt mit Gas die Henry-Konstante der Sättigungsdampfdruck psat ist, wird Gleichung 2.207 auch wie folgt angegeben:

Gleichung 2.208
wobei pd,equil,ref der Referenzdruck für den gelösten Gleichgewichtsmassenanteil ist. Dann wird Gleichung 2.204 neu geschrieben als:
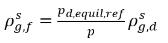
Gleichung 2.209
In Gleichung 2.202 und Gleichung 2.203 sind 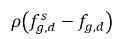 und
und 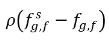 die Massenkonzentrationsunterschiede/-gradienten, die Antriebskräfte für die Absorption/Lösung und Freisetzung der nicht kondensierbaren Gase. Dies gibt an, dass der Transport des nicht kondensierbaren Gases über zwei Phasen erfordert, dass die Massenkonzentration ihren Gleichgewichtszustand verlässt. Die Richtung des Massenübergangs verschiebt das System hin zum Gleichgewicht, abhängig von lokalen und den dem Gleichgewicht entsprechenden Massenkonzentrationen in beiden Phasen. Aus dem Gleichgewichtsmodell ergibt sich Folgendes:
die Massenkonzentrationsunterschiede/-gradienten, die Antriebskräfte für die Absorption/Lösung und Freisetzung der nicht kondensierbaren Gase. Dies gibt an, dass der Transport des nicht kondensierbaren Gases über zwei Phasen erfordert, dass die Massenkonzentration ihren Gleichgewichtszustand verlässt. Die Richtung des Massenübergangs verschiebt das System hin zum Gleichgewicht, abhängig von lokalen und den dem Gleichgewicht entsprechenden Massenkonzentrationen in beiden Phasen. Aus dem Gleichgewichtsmodell ergibt sich Folgendes:
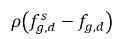 und
und 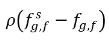 die Massenkonzentrationsunterschiede/-gradienten, die Antriebskräfte für die Absorption/Lösung und Freisetzung der nicht kondensierbaren Gase. Dies gibt an, dass der Transport des nicht kondensierbaren Gases über zwei Phasen erfordert, dass die Massenkonzentration ihren Gleichgewichtszustand verlässt. Die Richtung des Massenübergangs verschiebt das System hin zum Gleichgewicht, abhängig von lokalen und den dem Gleichgewicht entsprechenden Massenkonzentrationen in beiden Phasen. Aus dem Gleichgewichtsmodell ergibt sich Folgendes:
die Massenkonzentrationsunterschiede/-gradienten, die Antriebskräfte für die Absorption/Lösung und Freisetzung der nicht kondensierbaren Gase. Dies gibt an, dass der Transport des nicht kondensierbaren Gases über zwei Phasen erfordert, dass die Massenkonzentration ihren Gleichgewichtszustand verlässt. Die Richtung des Massenübergangs verschiebt das System hin zum Gleichgewicht, abhängig von lokalen und den dem Gleichgewicht entsprechenden Massenkonzentrationen in beiden Phasen. Aus dem Gleichgewichtsmodell ergibt sich Folgendes:◦ Gasabsorption/-lösung in eine Flüssigkeit – Ein Massenübergang findet aus der Gasphase (freies Gas) hin zur Flüssigphase (gelöstes Gas) statt. Das Gleichgewichtsmodell geht davon aus, dass das freie Gas an der Gasphase im Gleichgewichtszustand ist: 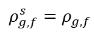 . Unter Verwendung von Gleichung 2.204 und Gleichung 2.209 ergibt sich Folgendes:
. Unter Verwendung von Gleichung 2.204 und Gleichung 2.209 ergibt sich Folgendes:
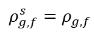 . Unter Verwendung von Gleichung 2.204 und Gleichung 2.209 ergibt sich Folgendes:
. Unter Verwendung von Gleichung 2.204 und Gleichung 2.209 ergibt sich Folgendes:
Gleichung 2.210
Aus Gleichung 2.202 und Gleichung 2.203 sind die Quellenterme für den Massenübergang die Folgenden:

Gleichung 2.211

Gleichung 2.212
◦ Gasfreisetzung aus einer Flüssigkeit – Ein Massenübergang findet aus der Flüssigphase (gelöstes Gas) hin zur Gasphase (freies Gas) statt. Bei diesem Prozess geht das Gleichgewichtsmodell davon aus, dass sich das gelöste Gas in der Flüssigphase immer im Gleichgewichtszustand befindet: 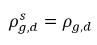 . Aus Gleichung 2.202, Gleichung 2.203, Gleichung 2.204 und Gleichung 2.209 ergeben sich folgende Massenübergangsraten:
. Aus Gleichung 2.202, Gleichung 2.203, Gleichung 2.204 und Gleichung 2.209 ergeben sich folgende Massenübergangsraten:
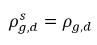 . Aus Gleichung 2.202, Gleichung 2.203, Gleichung 2.204 und Gleichung 2.209 ergeben sich folgende Massenübergangsraten:
. Aus Gleichung 2.202, Gleichung 2.203, Gleichung 2.204 und Gleichung 2.209 ergeben sich folgende Massenübergangsraten: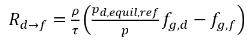
Gleichung 2.213
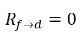
Gleichung 2.214
Beachten Sie, dass dann, wenn ein Teil des nicht kondensierbaren Gases in der Flüssigkeit gelöst ist, das frei expandierbare Gas nur der Teil ist, der in der Gasphase verbleibt, fg,f. Daher wird die Mischungsdichte wie folgt berechnet:
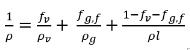
Gleichung 2.215
und der Volumenanteil des freien Gases ist wie folgt:
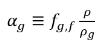
Gleichung 2.216