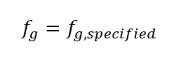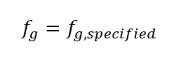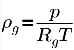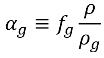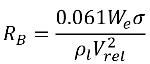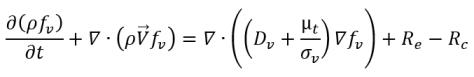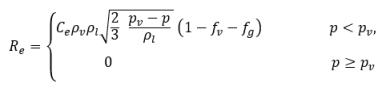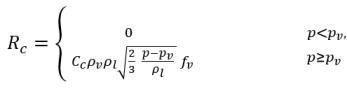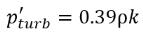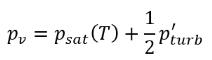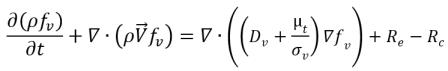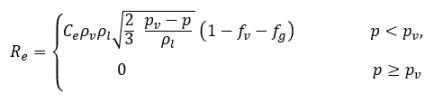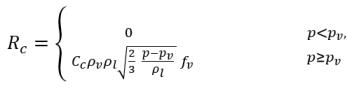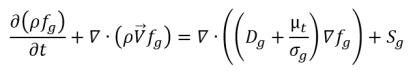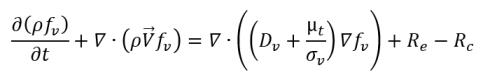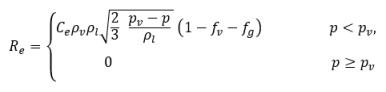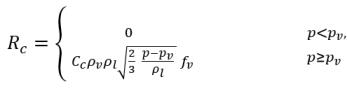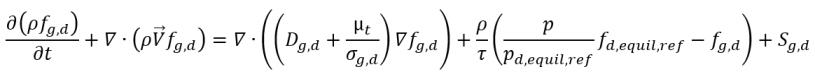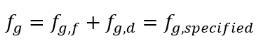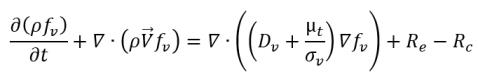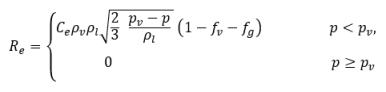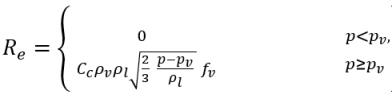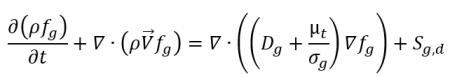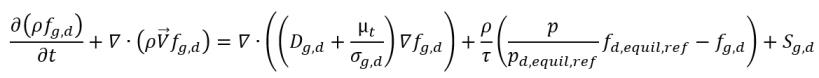Creo Flow Analysis では、元の Singhal ほかのモデルと同様に、キャビテーション発生を伴うフロー内の作動流体は常に、液体、蒸気、およびいくつかの非凝縮性気体の混合物であると見なされます。デフォルトでは、キャビテーションモデルは液体-蒸気相変化と非凝縮性気体の効果の両方から構成されています。非凝縮性気体効果のモデリングアプローチに基づいて、液体系におけるエアレーションとキャビテーションを予測する、以下の表に示す 5 つの異なるモデルが提供されています。このセクションでは、これらのモデルについて詳しく説明します。

気体質量分率一定モデルは、Creo Flow Analysis における基本またはデフォルトのキャビテーションモデルです。これは Singhal ほかによる研究に基づいています。このモデルでは、作動流体において、液体内に常に存在する非凝縮性気体 (NCG) は、不溶性気体、つまり理想気体の法則に従う自由な気泡であるものと見なされます。事前に指定されている非凝縮性気体はどれもキャビテーション発生域内の圧力低下に伴って自由膨張しますが、非凝縮気体の質量分率は事前に指定されており、キャビテーション発生を伴うフロー内において質量分率が常に一定となります。

式 2.217

ここで、fg,specified はユーザーが指定した値です。

非凝縮性気体の密度は理想気体の法則に従います。

式 2.218

ここで、T は流体温度であり、事前に指定されているか (等温フロー)、熱伝達が考慮される場合には混合物エネルギー保存式 2.168を解くことによって取得されます。式 2.173から、非凝縮気体の体積分率は以下のようになります。

式 2.219

NCG の質量分率は固定されており、通常は自然水において 1.5e-05 または 15 ppm という小さい値ですが、その体積分率αg は固定されておらず、より大きい値である場合があります。キャビティや低圧区域では、非凝縮性気体が蒸気と競合し、気体と蒸気の密度に応じて空間内の空隙を満たします。

液体-蒸気質量移動については、式 2.194と式 2.195が蒸気の質量分率式 2.169でキャビテーションのソース項とシンク項を構築するための基盤として使用されます。具体的には、気泡の成長と崩壊の両方において既知のフロー量を使用して気泡半径 RB が推定されなければなりません。Singhal ほかは、一般的な気泡サイズ RB が限界 (可能な最大の) 気泡サイズと同じである場合、RB は空気抵抗と表面張力のバランスによって決定されることを証明しました。原子力産業で使用されている相関関係は以下のとおりです。

式 2.220

ここで、Vrel は液体-蒸気の相対速度の大きさです。キャビテーションが発生する気泡流動領域では、Vrel は一般的に液体の速度に対して 5 % から 10 % 程度小さくなります。αv →0 としたときに RB →0 となるなどの各種極限引数を使用し、単位体積当りの相変化率はドナー相の体積分率 (または質量分率) に比例するという事実に基づき、蒸気の発生率/凝縮率を表す以下の式が得られ、キャビテーションモデルが完成します。

式 2.221

式 2.222

式 2.223

ここで、Ce は蒸発係数、Cc は凝縮係数であり、これらはユーザー指定の定数値 (デフォルトで 1.0 に設定) または既知のフロー量の関数です。式 2.222と式 2.223では、新しいしきい値圧力ρv が式 2.194および式 2.195の飽和蒸気圧ρsat の代わりに使用されます。Singhal ほかによると、実験的研究で観察されたキャビテーション発生を伴うフローにおける乱流の影響を反映させるために、Hinze によって与えられる乱流圧力変動のローカル値。

式 2.224

が飽和蒸気圧に加算され、相変化しきい値圧力値は以下のように提起されます。

式 2.225

層流の場合、pv=psat(T)

熱伝達が考慮され、すべての相 (液体、蒸気、非凝縮性気体) の密度が温度に従って変化する場合、飽和蒸気圧 psat も温度の関数となります。その結果、このキャビテーションモデルではキャビテーションに対する熱の直接的な影響が考慮されます。

気体質量分率可変モデルでは、非凝縮性気体が常に自由気体のままとなって液体に溶解することはないが、質量分率は気体質量分率一定モデルのように事前に定数として指定されないものとします。代わりに、局所的な質量分率の分布は輸送方程式によって支配されます。一方、液体-蒸気質量移動は、式 2.221、式 2.222、および式 2.223で参照されているキャビテーションモデルによってモデリングされます。わかりやすくするため、モデリング式の完全なセットを以下に示します。

キャビテーション発生を伴うフローでは、流体内の非凝縮性気体が液体に溶解するか、液体から非凝縮性気体が放出されることによって、液相と気相の間で質量濃度が動的平衡状態になります。平衡溶解気体モデルでは、合計非凝縮性気体の質量分率は一定のままであるものとします。ただし、その一部は液体に溶解して瞬時に局所平衡条件を満たします。数学的には、同じ蒸気質量分率式と蒸気質量移動モデルに加え、常に平衡状態にあるものとして溶解気体 fgd の質量分率に関する追加の輸送方程式が計算されます。モデリング式は以下のとおりです。

このモデルでは、液体内の溶解気体が常に平衡状態にあるという条件が緩和されます。溶解気体 (fg,d) の質量分率は、瞬時的な質量移動による平衡状態によって決まるのではなく、成分の輸送および溶解速度または放出速度 (有限速度) によって決まります。したがって、溶解気体モデルは平衡溶解気体モデルと同じモデリング式である式 2.230から式 2.234を共有します。ただし、気体が溶解および放出する際の質量移動の有限速度は別のタイムスケール (Γ) によって表されます。液体への気体の吸収または溶解については、指定されている吸収時間によってΓが与えられます (溶解気体の溶解時間はデフォルトでは 10 秒です)。液体から溶解した気体の放出については、指定されている気体放出時間によって質量移動の速度が決定されます (溶解気体の放出時間Γはデフォルトでは 10 秒です)。

全気体モデルは、溶解気体モデルと気体質量分率可変モデルの組み合わせです。非凝縮性気体質量分率は、時間および空間に応じて変化しますが、非凝縮性気体の場合、気体の溶解または吸収および放出も発生することがあります。モデリング式の完全なセットを以下に示します。