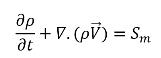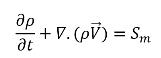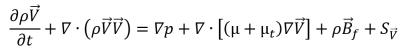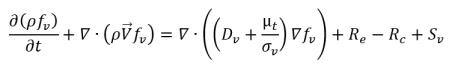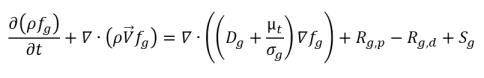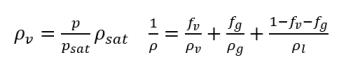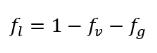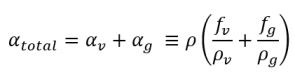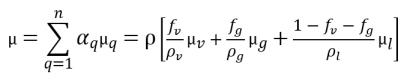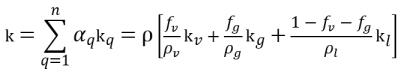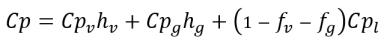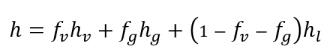支配方程式
キャビテーション輸送モデルでは、液体と気体 (蒸気とその他の予想される気体) の混合物のバルク運動は、可変密度の単相フローとして扱われます。混合物フローの一般支配方程式のセットは、複数成分フローと同じであるのに対し、輸送方程式はキャビテーション内で発生する蒸気の質量分率を支配するように特別に構成されています。非凝縮性気体の影響をモデリングするため、気体モデルに応じて、気体の質量分率の追加の輸送方程式も計算します。キャビテーション発生を伴うフローについて計算される一般支配方程式の完全なセットを以下に示します。
• 連続性
式 2.166
ここで、Sm は、キャビテーションから独立した正味の外部ソースまたはユーザーソースです
• 運動量方程式
式 2.167
• エネルギー方程式
式 2.168
• 蒸気の質量分率の式
式 2.169
ここで、
fv | 蒸気の質量分率 |
Re | 蒸気発生ソース (蒸発) |
Rc | シンク項 (凝縮) |
Sv | 外部またはユーザー定義の蒸気のソース項 |
• 非凝縮性気体 (NCG) の質量分率の式
式 2.170
これは非凝縮性気体 (NCG) の一般輸送方程式であり、発生項、シンク項、および外部またはユーザー定義のソース項から成ります。
キャビテーションモデルに応じて、いくつかの異なる式 (ゼロと 2 の間) を非凝縮性気体、溶解気体などとして計算します。
乱流フローの場合、乱流粘度μ
t は乱流モデリング式を計算することによって求められます。乱流
Prandtl 数σ
t、σ
v、σ
g は事前に指定されているモデルパラメータです。乱流モデルの詳細については
乱流モジュールで説明しています。
輸送方程式で、混合物のプロパティは以下の関係式を使用して計算されます。
• 混合物密度
式 2.171
ここで、
ρv | 蒸気の密度 |
ρg | 非凝縮性自由気体の密度 |
ρl | 液体の密度 |
液体および蒸気密度は、一定 (非圧縮性)、可変 (圧縮性)、またはその両方です。これに対し、キャビテーションモデルにおいて、非凝縮性自由気体の密度は常に理想気体であるものと見なされます。
式 2.171では、すべての成分の質量分率の合計は 1 であるという物理的な制約条件を使用して液体の質量分率 ƒ
l が計算されています。つまり、
式 2.172
キャビテーション発生を伴うフローでは、対象パラメータは蒸気の体積分率αv または気相の体積分率の合計αtotal であり、これは計算された質量分率 ƒv と自由気体の質量分率 ƒg から導かれます。
式 2.173
式 2.174
• 混合物粘度
式 2.175
ここで、
• 混合物熱特性
式 2.176
式 2.177
式 2.178
ここで、
k | 熱伝導率 |
Cp | 定圧プロセスでの比熱 |
h | 比エンタルピー |
関連する各成分は下付き添字によって示されています (蒸気は v、非凝縮性自由気体は g、液体は l)。