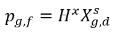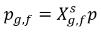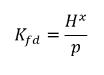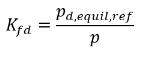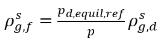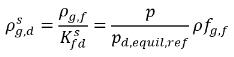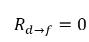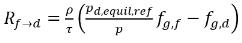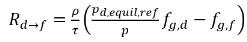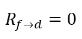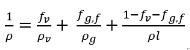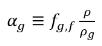キャビテーションモデルの理論
蒸気の輸送
方程式 2.169において、R
e と R
c は、キャビテーション発生を伴うフロー内の蒸気の気泡の成長と崩壊に関連する質量移動のソース項です。これらの項は、キャビテーションプロセス中の蒸気相と液相間の質量交換を表します。R
e と R
c は、液体内の単一の蒸気の気泡の成長を説明する
レイリー-プレセット方程式でモデリングされます。
液体-蒸気質量移動
キャビテーションにおける正味の相変化率の式を導くため、非凝縮性気体を考慮しない、すべり速度がゼロである非圧縮性液体-気体 2 相フローを考えます。液体から蒸気への正味の質量移動率を R で表した場合、液体と蒸気の体積分率の式と総質量の連続方程式は以下のようになります。
• 液相
式 2.179
• 蒸気相
式 2.180
• 混合物 (総質量連続性)
式 2.181
液体-蒸気 2 相系では、混合物の密度ρは蒸気の体積分率と相密度によって表されます。
式 2.182
液体密度と蒸気密度のどちらも一定である (非圧縮性) と見なされるので、速度勾配と蒸気の体積分率の関係式は
式 2.181と
式 2.182から導かれます。
式 2.183
式 2.179と
式 2.183を組み合わせることで、以下のような正味質量のソース項の式が与えられます。
式 2.184
式 2.184を
式 2.180に代入すると、蒸気の体積分率の式は以下の一般形式に書き換えられます。
式 2.185
蒸気の質量分率と体積分率の関係式である
式 2.173を適用することで、蒸気の質量分率を使用して
式 2.185を表すことができます。
式 2.186
式 2.185と
式 2.186から、液相と蒸気相の間の速度すべりがゼロの状態においては、キャビテーションを、追加の蒸気質量分率輸送方程式を使用して単相フローとして、または液体-蒸気質量移動がある
オイラー多相混合物フローとしてモデリングできることがわかります。拡散の影響と相の速度差を考慮しない場合、この 2 つのアプローチは数学的に同一です。
Creo Flow Analysis はキャビテーション発生を伴うフローのモデリングに単相アプローチを採用しています。
気泡力学の考慮事項
ほとんどの自然環境とエンジニアリングのシステムにおいて、キャビテーションが発生するのに十分な数の核 (気泡や非凝縮性気体など) が液体内に存在します。この結果、キャビテーションプロセスをモデリングするには、気泡の成長と崩壊を正しく考慮することに主な重点が置かれます。流動液体において、液体と蒸気気泡の間の速度すべりがゼロであるとした場合、気泡の力学方程式は、液体内の気泡の成長を説明するレイリー-プレセットの一般式から導かれます。
式 2.187
ここで、
RB | 気泡半径 |
pB | 気泡内の圧力 (ほかの気体が存在しない状態での液体温度における蒸気圧とします) |
p | 気泡周囲の液体内の圧力 |
σ | 液体と蒸気の間の表面張力係数 |
この式は力学的平衡 (気泡の成長に対する熱の障壁がない) から導かれます。
2 次時間微分 (低振動周波数に対応)、粘性減衰項、表面張力を無視した場合、漸近状態で有効な
式 2.187は以下のようにまとめられます。
式 2.188
このまとめた
レイリー-プレセットの式は、気泡力学の影響をキャビテーションモデルに導入するための物理的なアプローチを提供します。気泡半径は (p
B-p) の応じて増減します。つまり、気泡は p<p
B の場合は成長し、p>p
B の場合は崩壊します。したがって、
式 2.188は以下のように書き換えられます。
式 2.189
ηを液体内の蒸気気泡数密度 (単位体積当りに存在する気泡の数) とし、すべての蒸気気泡が同じ半径 RB を持つ完全な球であるとした場合、蒸気相の体積分率は以下のようになります。
式 2.190
蒸気気泡は液体内で作成または破壊されないが、キャビテーションプロセス中に気泡は成長 (蒸発) および崩壊 (凝縮) できるものとします。
式 2.190では、蒸気気泡数密度 (η) は一定のままとなりますが、気泡半径 (R
B) は増減します。その結果、蒸気の体積分率の時間微分は以下のように計算されます。
式 2.191
式 2.191を
式 2.186に代入すると、蒸気相の質量分率を支配する以下のような輸送方程式が与えられます。
式 2.192
式 2.189を適用することで、液体と蒸気の間の単位ボリューム当りの質量移動の正味速度は以下の形式をとります。
式 2.193
ここで、
式 2.193は、キャビテーションにおいては、単位ボリュームの質量移動速度 (R) は蒸気相と液相の密度の関数であり (これらの密度に比例)、混合物の密度に反比例する、ということを示しています。
式 2.192は相と混合物の質量連続性から直接導かれるので、この式は厳密であり、キャビテーションにおける液相と蒸気相の間の質量移動を正確に表します。気泡力学の導入によって、
式 2.193は同様のアプローチを使用して、液体から蒸気への質量移動 (気泡の成長、つまり蒸発) と蒸気から液体への質量移動 (気泡の崩壊、つまり凝縮) の 2 つの物理的に正反対であるプロセスをモデリングします。蒸気の質量分率の輸送
方程式 2.192では、気泡の成長がソース項、気泡の崩壊がシンク項として扱われます。
実際のキャビテーションモデルでは、通常、局所遠方界圧力 p はセル中央の圧力と同じであるものと見なされます。溶解気体、質量移動、粘性減衰がない場合、気泡圧力 pB は飽和蒸気圧 (psat、材料特性) と等しくなります (pB=psat)
式 2.192と
式 2.193を一般的な蒸気の質量分率の
式 2.169と比較した場合、ソース項 R
e と R
c は以下のようになります。
• フローの局所圧力が飽和蒸気圧より低い場合 (p<psat)、蒸発のみが発生して以下のようになります。
式 2.194
• フローの局所圧力が飽和蒸気圧より高い場合 (p>psat)、凝縮のみが発生します。
式 2.195
式 2.194と
式 2.195は、ほぼすべての力学的 2 相キャビテーションモデルの基礎となります。
Creo Flow Analysis は
Singhal ほかのモデリングアプローチを使用しています。
気体の吸収/溶解および放出
非凝縮性気体は、作動流体内によく存在し、キャビテーションに大きな影響を与えることがあります。非凝縮性気体がフローとともに自由に移動し、液体に溶解したり液体から放出されることによって、自然に液相と気相の間で質量濃度が動的平衡状態になることもあります。液体への気体の吸収/溶解と放出は、液体-気体の質量移動の現象でもあり、質量濃度の差と勾配によって決まります。キャビテーション発生を伴うフローをモデリングするには、非凝縮性気体の影響と、混合物のフローにおいて考えられる液体-気体の質量移動も考慮する必要があります。
液体-気体 2 相フローにおいて、空気や酸素などの非凝縮性気体が液相 (溶解気体) と気相 (自由気体) の両方に存在するとした場合、各相における気体の質量分率の輸送方程式は以下のようになります。
• 自由気体 (気相)
式 2.196
• 溶解気体 (液相)
式 2.197
ここで、
fg,f | 自由気体の質量分率 |
fg,d | 自由気体と溶解気体の質量分率 |
Sg,f、Sg,d | 外部またはユーザー定義のソース |
Dg,f | 自由気体と溶解気体の拡散率 |
Dg,d | 溶解気体の拡散率 |
非凝縮性気体の質量分率を fg とした場合、以下のようになります。
fg=fg,f
または、以下の式を解くことによって、空間と時間におけるその輸送の解が得られます。
式 2.199
2 つの相が接触している場合、一方の相からもう一方の相に移動している自由気体 f と溶解気体 d は 2 相間で動的平衡状態になろうとします。平衡モデルでは、質量移動の体積速度は質量濃度の勾配または差によって決まるものとします。
式 2.200
式 2.201
ここで、
AI | 液体-気体界面面積 |
kf,d(=kd,f) | バルク体積質量移動係数 |
ρg,d(=ρfg,d) | 溶解気体の局所質量濃度 |
ρg,f(=ρfg,f) | 自由気体の局所質量濃度 |
| 溶解気体のそのホスト相における平衡質量濃度 |
| 自由気体のそのホスト相における平衡質量濃度 |
式 2.202
式 2.203
一般的に、
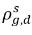
と
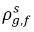
は同じではありません (不連続性)。この 2 つの濃度間には、温度、圧力、混合物の組成によって決まる well-defined な平衡曲線があります。この曲線は通常は単調で非線形であり、係数
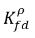
を使用した準線形関係式として表されることが一般的です。
式 2.204
ここで、K
f,d は通常、物理法則または経験的相関式を使用して決定されます。一般的なアプローチとしては、一般化された平衡関係を与える
ヘンリーの法則に従います。これは、気相と接触する液体混合物において、自由気体の分圧ρ
g,f は、液相における溶解気体の平衡モル分率
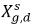
とヘンリーの定数 H
x の積と等しいことを示しています。
式 2.205
自由気体の相が理想気体の法則に従う場合、ダルトンの分圧の法則によって以下の式が与えられます。
式 2.206
式 2.207
したがって、ヘンリーの定数は圧力の単位を持ち、基準圧力と見なされます。気体と接触する理想液体混合物では、ヘンリーの定数は飽和蒸気圧 p
sat であり、したがって
式 2.207を以下のように表すこともできます。
式 2.208
ここで、p
d,equil,ref は溶解平衡質量分率の基準圧力です。その結果、
式 2.204は以下のように書き換えられます。
式 2.209
式 2.202と
式 2.203において、
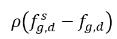
と
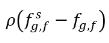
は、質量濃度の差/勾配であり、非凝縮性気体の吸収/溶解と放出の推進力です。これは、2 相間で非凝縮性気体が移送されるためには、質量濃度が平衡状態から逸脱しなければならないことを示しています。両方の相における局所質量濃度と平衡質量濃度に応じた方向に質量移動が生じることで、系が平衡状態に移ります。平衡モデルからは、以下のようになります。
◦ 液体への気体の吸収/溶解 - 気相 (自由気体) から液相 (溶解気体) への質量移動が発生します。平衡モデルでは、気相の自由気体は平衡状態であるものとします:
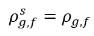
。
式 2.204と
式 2.209を使用して、以下が与えられます。
式 2.210
式 2.211
式 2.212
◦ 液体からの気体の放出 - 液相 (溶解気体) から気相 (自由気体) への質量移動が発生します。このプロセスでは、平衡モデルの場合、液相内の溶解気体が常に平衡状態にあるものとします。
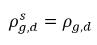 式 2.202
式 2.202、
式 2.203、
式 2.204、および
式 2.209から、質量移動の速度は以下のようになります。
式 2.213
式 2.214
非凝縮性気体の一部が液体に溶解した場合、気相には自由膨張可能な気体 fg,f が一部だけ残ります。したがって、混合物の密度は以下のように計算されます。
式 2.215
さらに、自由気体の体積分率は以下のようになります。
式 2.216
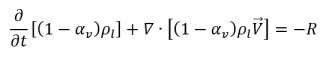
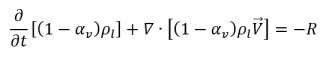
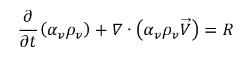

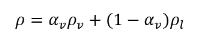
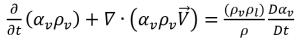
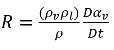
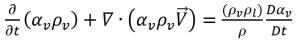
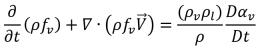
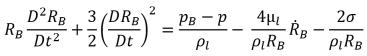
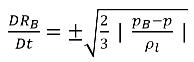
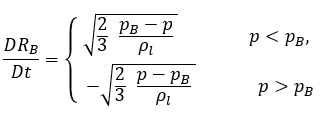
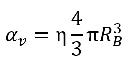
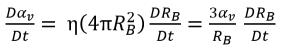
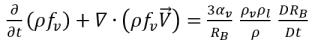
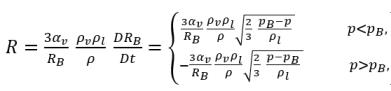
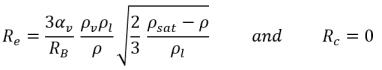
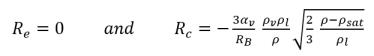
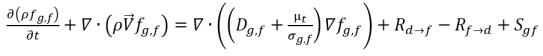
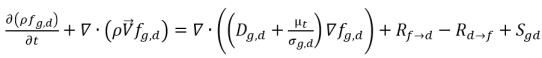
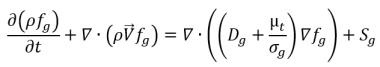
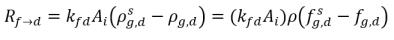
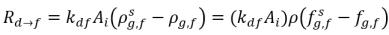
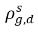
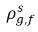
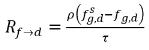
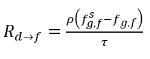
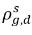 と
と 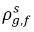 は同じではありません (不連続性)。この 2 つの濃度間には、温度、圧力、混合物の組成によって決まる well-defined な平衡曲線があります。この曲線は通常は単調で非線形であり、係数
は同じではありません (不連続性)。この 2 つの濃度間には、温度、圧力、混合物の組成によって決まる well-defined な平衡曲線があります。この曲線は通常は単調で非線形であり、係数 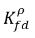 を使用した準線形関係式として表されることが一般的です。
を使用した準線形関係式として表されることが一般的です。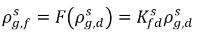
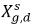 とヘンリーの定数 Hx の積と等しいことを示しています。
とヘンリーの定数 Hx の積と等しいことを示しています。