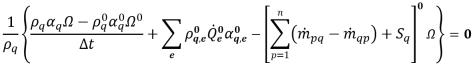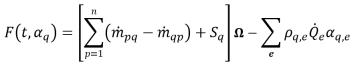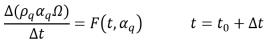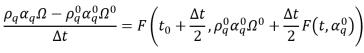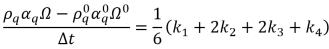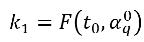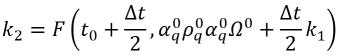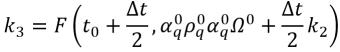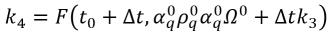Considérations numériques
Dans les modèles multiphases homogènes qui ne prennent pas en compte les différences de vitesse de glissement, aucun traitement spécial n'est requis pour résoudre les équations d'énergie cinétique du mélange et la formulation du flux de volume à travers la face. Ceci s'explique par le fait qu'il s'agit des mêmes équations que celles qui régissent les écoulements monophasiques à densité variable. Cette rubrique est axée sur la construction de l'équation de correction de pression et sur le traitement des équations de fraction volumique de phase, en particulier les schémas de résolution d'interface dans le modèle VOF.
Equation de continuité du volume
Pour satisfaire à la contrainte de continuité et garantir la stabilité numérique, l'équation de correction de pression repose sur la continuité du volume total plutôt que sur celle de la masse. Lorsque vous divisez l'
équation 2.57 continuité de n
ième phase q / fraction volumique par une densité de référence de phase, ρ
rq, et que vous combinez toutes ces phases, vous obtenez une équation de continuité du volume total conforme à la loi de conservation de la masse :
équation 2.135
où la densité de référence de phase est généralement définie en tant que densité de phase, ρrq = ρq.
L'introduction du terme Ω correspondant au volume d'une cellule de calcul et l'intégration de l'
équation 2.135 au-dessus du volume de contrôle génèrent les équations algébriques discrétisées :
équation 2.136
Si vous utilisez la même approche que dans le solveur basé sur la pression monophasique décrit dans la section Numerics et que vous partez des hypothèses suivantes :
équation 2.137
équation 2.138
vous pouvez réorganiser l'
équation 2.136 sous la forme de l'équation de correction suivante :
équation 2.139
Ici, * et ’ représentent les anciennes valeurs et les corrections.
Δt | Pas de temps |
Ae | Zone au niveau de la face e |
| Flux de volume |
En suivant la même approche que dans le solveur basé sur la pression monophasique, appliquez les algorithmes de type SIMPLE (Simple, SimpleC et SimpleS) pour relier les corrections de vitesse et de pression et pour obtenir l'équation de correction de pression relative aux écoulements multiphasiques :
équation 2.140
où,
Anb | Coefficient de liaison |
Sp | Terme linéarisé |
Equations de fraction volumique de phase
Le transport d'une fraction volumique de phase est régi par la conservation de la masse de phase. Etant donné que la conservation du volume total est appliquée par la formulation de l'équation de correction de pression, les équations réelles résolues pour les fractions volumiques de phase se présentent également sous forme de conservation du volume afin de garantir la cohérence numérique :
équation 2.141
Généralement, dans le cas d'un système à n phases, seules les équations (n–1) sont résolues, alors que la nième phase est obtenue à partir de la contrainte physique :
équation 2.142
Si l'on applique l'approche de discrétisation, la forme intégrale de l'
équation 2.141 est la suivante :
équation 2.143
Tels qu'indiqués dans les équations de conservation de l'énergie cinétique, de l'énergie et du volume total, les schémas de discrétisation spatiale et temporelle jouent un rôle crucial pour la précision numérique. Pour les équations de fraction volumique, outre les schémas temporels implicites standard, une pratique courante consiste à utiliser le pas de temps explicite avec des schémas d'advection haute résolution, ce qui vous permet de capturer plus précisément les interfaces dans les modèles VOF. Les formulations VOF implicites et explicites sont décrites en détail dans cette section.
• Formulation VOF implicite
Dans le cas de la formulation VOF implicite, l'équation de fraction volumique de phase discrétisée présente l'expression générale suivante :
équation 2.144
Dans cette équation, la fraction volumique de phase α
q au pas de temps actuel est une fonction d'autres grandeurs au pas de temps actuel. Par conséquent, de même que les équations de correction de pression, d'énergie cinétique et d'énergie, l'
équation 2.144 de fraction volumique discrétisée est résolue de manière itérative à chaque pas de temps. Dans
Creo Flow Analysis, la formulation implicite adoptée se résume comme suit :
◦ Schémas d'advection : le flux volumétrique
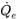
est calculé en fonction du champ d'écoulement au pas de temps actuel. La valeur de face α
q,e est approximée en termes de valeurs de centre de cellule α
q,P,α
q,E et de gradients (
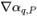
,
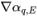
) des cellules voisines P et E. Comme dans l'équation scalaire passive, les schémas d'advection prennent la forme générale suivante :
équation 2.145
Lorsque l'on utilise des valeurs distinctes pour les paramètres γ, βP et βE, ainsi que les schémas pour calculer les gradients de fraction volumique, quatre schémas d'advection sont développés pour les équations de fraction volumique : Décentré de premier ordre, Décentré de second ordre, Différence centrée et Haute résolution.
◦ Schémas temporels : pour décrire le schéma temporel implicite, vous pouvez généraliser l'
équation 2.144 dans l'expression suivante :
équation 2.146
Les variables dépourvues d'exposant correspondent aux valeurs au pas de temps actuel. Les variables dotées de l'exposant 0 ou 00 indiquent les valeurs aux pas de temps précédents.
Les paramètres β et βCN varient entre 0 et 1 et déterminent les schémas temporels. Plus précisément, trois schémas temporels sont adoptés pour la discrétisation des équations de fraction volumique de phase :
▪ Schéma décentré de premier ordre d'Euler : β = 0, βCN = 1
▪ Schéma de second ordre à trois niveaux : β = 0, βCN = 1
▪ Méthode de Crank-Nicolson : β = 0, βCN = 0.6 (par défaut)
• Formulation VOF explicite
Lorsque l'on utilise la formulation explicite pour la résolution des équations VOF, les fractions volumiques de phase au pas de temps actuel sont directement calculées en fonction des grandeurs connues à partir du pas de temps précédent. Par conséquent, la formulation VOF explicite ne nécessite pas de solution itérative pour l'
équation 2.144 lors de chaque pas de temps. Toutefois, étant donné que les autres équations de transport sont résolues implicitement, le pas de temps utilisé pour le calcul de la fraction volumique est généralement plus faible que celui des autres équations de transport. La formulation VOF explicite impose la détermination d'un sous-pas de temps, qui est calculé automatiquement ou que vous pouvez fournir dans
Creo Flow Analysis.
Avec la formulation explicite, l'équation de fraction volumique de phase discrétisée se présente comme suit :
équation 2.147
où les termes d'advection et de source sont calculés en fonction des grandeurs connues à partir du pas de temps précédent. Le flux volumétrique
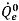
est calculé de la même manière que
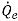
dans la formulation implicite. La fraction volumique de face
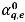
peut également être estimée à l'aide de l'un des quatre schémas d'advection : Décentré de premier ordre, Décentré de second ordre, Différence centrée et Haute résolution.
Creo Flow Analysis propose les trois algorithmes ci-après pour les schémas de pas de temps explicites :
• Algorithme explicite de premier ordre d'Euler : l'équation de fraction volumique est discrétisée comme suit :
équation 2.148
• Algorithme de second ordre de Runge-Kutta : introduit la fonction suivante :
équation 2.149
équation 2.150
Le schéma explicite de second ordre de Runge-Kutta présente la forme suivante :
équation 2.151
• Algorithme de quatrième ordre de Runge-Kutta : pour l'équation de fraction volumique de phase q, le schéma explicite de quatrième ordre de Runge-Kutta se présente comme suit :
équation 2.152
où
équation 2.153
équation 2.154
équation 2.155
équation 2.156
Dans le cas du système à n phases, seules les fractions volumiques de phase (n-1) sont généralement résolues, et la fraction restante est obtenue à partir de la contrainte physique,
équation 2.142. Toutefois, vous pouvez également résoudre toutes les équations de fraction volumique de phase n, et satisfaire l'
équation 2.142 en pondérant chaque phase à l'aide de la somme de la fraction volumique totale calculée. Cette dernière peut être inférieure ou supérieure à 1 dans un processus itératif.
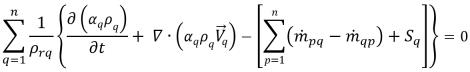
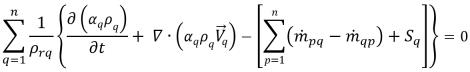
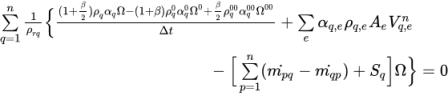
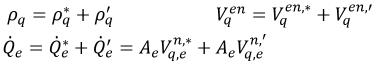
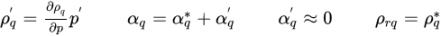
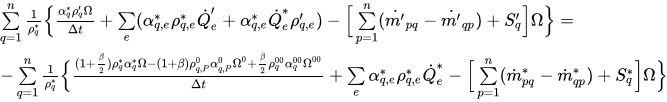
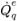
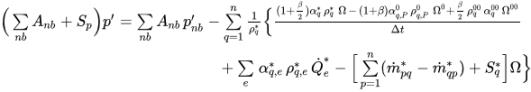
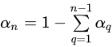
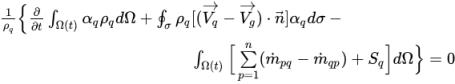
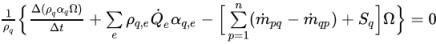
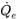 est calculé en fonction du champ d'écoulement au pas de temps actuel. La valeur de face αq,e est approximée en termes de valeurs de centre de cellule αq,P,αq,E et de gradients (
est calculé en fonction du champ d'écoulement au pas de temps actuel. La valeur de face αq,e est approximée en termes de valeurs de centre de cellule αq,P,αq,E et de gradients (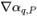 ,
,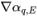 ) des cellules voisines P et E. Comme dans l'équation scalaire passive, les schémas d'advection prennent la forme générale suivante :
) des cellules voisines P et E. Comme dans l'équation scalaire passive, les schémas d'advection prennent la forme générale suivante :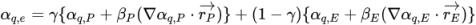
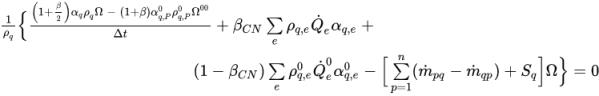
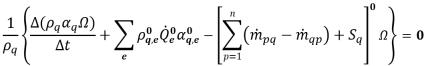
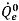 est calculé de la même manière que
est calculé de la même manière que 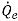 dans la formulation implicite. La fraction volumique de face
dans la formulation implicite. La fraction volumique de face 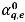 peut également être estimée à l'aide de l'un des quatre schémas d'advection : Décentré de premier ordre, Décentré de second ordre, Différence centrée et Haute résolution.
peut également être estimée à l'aide de l'un des quatre schémas d'advection : Décentré de premier ordre, Décentré de second ordre, Différence centrée et Haute résolution.