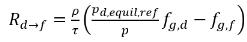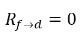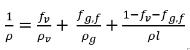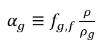Modèles de la théorie de cavitation
Dans
l'équation 2.169 relative au transport de la vapeur, les valeurs R
e et R
c correspondent aux termes du transfert massique liés à la croissance et à l'effondrement des bulles de vapeur dans les écoulements cavitants. Ces termes expliquent l'échange de masse entre les phases liquide et vapeur lors du processus de cavitation. Les valeurs R
e et R
c sont modélisées selon l'équation de
Rayleigh-Plesset, qui décrit la croissance d'une bulle de vapeur dans un liquide.
Transfert de masse entre les phases liquide et vapeur
Pour dériver une expression de la fréquence de changement de phase instantanée lors de la cavitation, appuyez-vous sur un écoulement à deux phases liquide/vapeur présentant une vélocité sans glissement, sans tenir compte des gaz non condensables. Si vous introduisez la valeur R pour représenter le débit instantané du transfert de masse entre les phases liquide et vapeur, les équations des fractions volumiques de la vapeur et du liquide ainsi que l'équation de continuité de la masse totale sont indiquées comme suit :
• Phase liquide
équation 2.179
• Phase vapeur
équation 2.180
• Mélange (continuité de la masse totale)
équation 2.181
Dans le système à deux phases liquide/vapeur, la masse volumique du mélange ρ est exprimée en termes de densité de phase et de masse volumique de la fraction volumique de la vapeur :
équation 2.182
Comme la masse volumique du liquide et de la vapeur est supposée constante (incompressible), une relation entre le gradient de vitesse et la fraction volumique de la vapeur est dérivée de l'
équation 2.181 et de l'
équation 2.182 :
équation 2.183
En combinant l'
équation 2.179 et l'
équation 2.183, vous obtenez l'expression du terme de la source de masse instantanée comme suit :
équation 2.184
En remplaçant l'
équation 2.184 dans l'
équation 2.180, l'équation relative à la fraction volumique de la vapeur est reformulée sous la forme générale :
équation 2.185
En appliquant la relation entre la fraction massique et la fraction volumique de la vapeur dans
l'équation 2.173, vous disposez de
l'équation 2.185 en termes de fraction massique de la vapeur :
équation 2.186
D'après l'
équation 2.185 et l'
équation 2.186, il apparaît ce qui suit : dans une condition de vélocité sans glissement entre les phases liquide et vapeur, la cavitation est modélisée sous la forme d'un écoulement à une seule phase, avec une équation de transport supplémentaire pour la fraction massique de la vapeur, ou sous la forme d'un mélange d'écoulement multiphase de type
eulérien avec un transfert de masse liquide/vapeur. Si l'on ne tient pas compte de l'effet de la diffusion et de la différence de vélocité entre les deux phases, les deux méthodes sont identiques sur le plan mathématique.
Creo Flow Analysis utilise l'approche à une seule phase pour modéliser les écoulements cavitants.
Prise en compte de la dynamique des bulles
Pour la plupart des occurrences naturelles et des systèmes d'ingénierie, le nombre de noyaux (bulles, gaz non condensables, etc.) dans le liquide est suffisant pour générer la cavitation. Ainsi, lors de la modélisation du processus de cavitation, l'accent est principalement mis sur la prise en compte adéquate de la croissance et de l'effondrement des bulles. Si l'on part du principe que, dans un liquide en écoulement, la vélocité des bulles de liquide et de vapeur ne présente aucun glissement, l'équation définissant la dynamique des bulles est dérivée de l'équation Rayleigh-Plesset généralisée qui décrit la croissance d'une bulle de gaz dans un liquide :
équation 2.187
où,
RB | rayon de la bulle |
pB | pression dans la bulle (on part du principe qu'il s'agit de la pression de la vapeur à la température du liquide, en l'absence d'autres gaz) |
p | pression du liquide entourant la bulle |
σ | coefficient de tension de surface entre le liquide et la vapeur |
Cette équation est dérivée de l'équilibre mécanique (sans barrière thermique s'opposant à la croissance des bulles).
Si vous négligez la dérivée temporelle du second ordre (adaptée aux fréquences d'oscillation faibles), le terme d'amortissement visqueux et la force de tension de surface, vous disposez d'une expression réduite de l'
équation 2.187 qui peut être appliquée pour l'état asymptotique :
équation 2.188
Cette équation de
Rayleigh-Plesset réduite propose une approche physique qui introduit les effets de la dynamique des bulles dans les modèles de cavitation. Le rayon des bulles peut augmenter ou diminuer en fonction des signes de l'équation (p
B–p) : la bulle se développe si la valeur p est inférieure à p
B et elle s'effondre lorsque cette valeur est supérieure à p
B. L'
équation 2.188 est donc réécrite comme suit :
équation 2.189
Si la valeur η correspond à la densité des bulles de vapeur dans un liquide (nombre de bulles par volume unitaire), et si toutes les bulles de vapeur sont des sphères parfaites présentant le même rayon RB, la fraction volumique de la phase vapeur se présente comme suit :
équation 2.190
Il est supposé que les bulles de vapeur ne peuvent pas être créées ou détruites dans un liquide, mais qu'elles peuvent se développer (évaporation) et s'effondrer (condensation) durant un processus de cavitation. Dans l'
équation 2.190, la densité des bulles de vapeur (η) demeure une constante, mais le rayon des bulles (R
B) augmente ou diminue. La dérivée temporelle de la fraction volumique de la vapeur est calculée ainsi :
équation 2.191
En remplaçant
l'équation 2.191 dans
l'équation 2.186, on obtient l'équation de transport régissant la fraction massique de la phase vapeur :
équation 2.192
Si l'on applique
l'équation 2.189, le débit instantané du transfert de masse par volume unitaire entre les phases liquide et vapeur prend la forme suivante :
équation 2.193
où
l'équation 2.193 indique ce qui suit : dans la cavitation, le taux de transfert de masse pour chaque volume unitaire (R) est une fonction de (proportionnelle à) la densité de phase de la vapeur comme du liquide. Par ailleurs, il est inversement proportionnel à la masse volumique du mélange. Comme
l'équation 2.192 est dérivée directement des continuités de masse du mélange et des phases, elle est suffisamment précise pour représenter de manière exacte le transfert de masse entre les phases liquide et vapeur lors de la cavitation. Avec l'introduction de la dynamique des bulles, l'
équation 2.193 utilise une approche similaire pour modéliser les deux processus de transfert de masse, à la fois opposés et physiquement différents : du liquide vers la vapeur (croissance ou évaporation des bulles) et de la vapeur vers le liquide (effondrement des bulles ou condensation). Pour
l'équation 2.192 qualifiant le transport de fraction massique de la vapeur, la croissance des bulles est un terme source, alors que l'effondrement des bulles est considéré comme un terme puits.
Dans les modèles de cavitation pratiques, la pression locale au niveau du champ lointain p est généralement supposée identique à la pression du centre de la cellule. La pression des bulles pB est égale à la pression de la vapeur de saturation (psat, propriété du matériau) en l'absence de gaz dissous, de transport de masse et d'amortissement visqueux : pB=psat
Si l'on compare l'
équation 2.192 et l'
équation 2.193 avec l'
équation 2.169 générale, relative à la fraction massique de la vapeur, les termes sources R
e et R
c sont les suivants :
• Si la pression locale de l'écoulement est inférieure à la pression de la vapeur de saturation, p<psat, seule une évaporation se produit, de sorte que :
équation 2.194
• Si la pression locale de l'écoulement est supérieure à la pression de la vapeur de saturation, p>psat, seule une condensation se produit :
équation 2.195
L'équation 2.194 et
l'équation 2.195 constituent la base de presque tous les modèles de cavitation mécaniques à deux phases disponibles.
Creo Flow Analysis s'appuie sur l'approche de modélisation de
Singhal et autres.
Absorption/dissolution et libération des gaz
Les gaz non condensables sont souvent présents dans un fluide en mouvement, et peuvent avoir un impact important sur la cavitation. Parfois un gaz non condensable est librement transporté par l'écoulement, et se dissout naturellement dans un liquide (ou s'en libère) afin de créer un équilibre dynamique entre les concentrations massiques lors du passage à une phase liquide ou gazeuse. L'absorption de gaz ou sa dissolution et sa libération dans un liquide sont également des phénomènes de transfert de masse du liquide/gaz, régis par les gradients et différences en matière de concentration massique. Pour modéliser des écoulements cavitants, il est nécessaire de prendre en compte l'effet des gaz non condensables et l'éventuel transfert de masse du liquide/gaz dans le mélange d'écoulement.
Nous partons du principe suivant : dans un écoulement liquide/gaz à deux phases, un gaz non condensable tel que l'air ou l'oxygène est présent à la phase liquide (gaz dissous) ainsi qu'à la phase gazeuse (gaz libre). Ainsi, les équations de transport de la fraction massique du gaz à chaque phase sont les suivantes :
• Gaz libre (phase gazeuse)
équation 2.196
• Gaz dissous (phase liquide)
équation 2.197
où,
fg,f | fractions massiques du gaz libre |
fg,d | fractions massiques des gaz libre et dissous |
Sg,f, Sg,d | sources externes ou définies par l'utilisateur. |
Dg,f | diffusivité des gaz libre et dissous |
Dg,d | diffusivité du gaz dissous |
Si la fraction massique d'un gaz non condensable est décrite au préalable ainsi : fg, vous obtenez :
fg=fg,f
ou vous obtenez sa valeur de transport spatial et temporel en résolvant l'équation suivante :
équation 2.199
Dans l'
équation 2.196 et l'
équation 2.197, la source R
d→f indique le taux de libération des gaz dissous et R
f→d indique le taux d'absorption ou de dissolution des gaz libres.
Lorsque les deux phases sont en contact, les gaz libres f et les gaz dissous d ont tendance à se transporter d'une phase à l'autre afin d'établir un équilibre dynamique entre les deux phases. Les modèles d'équilibre supposent que les débits volumétriques des transferts de masse dépendent des différences ou des gradients relatifs à la concentration massique :
équation 2.200
équation 2.201
où,
AI | aire interfaciale liquide/gaz |
kf,d(=kd,f) | coefficient de transfert de masse volumétrique en masse |
ρg,d(=ρfg,d) | concentrations de masse locales du gaz dissous |
ρg,f(=ρfg,f) | concentrations de masse locales du gaz libre |
| concentrations de masse à l'équilibre du gaz dissous lors de ses phases d'accueil |
| concentrations de masse à l'équilibre du gaz libre lors de ses phases d'accueil |
Notez que
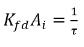
est associé à l'unité de temps inversé (1/s), un indicateur de l'efficacité du transfert de masse. Par conséquent, l'
équation 2.200 et l'
équation 2.201 ont également les formes suivantes :
équation 2.202
équation 2.203
En général,
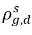
et
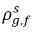
ne sont pas identiques (discontinuité). Il existe une courbe bien définie représentant l'équilibre entre les deux concentrations. Elle dépend de la température, de la pression et des compositions du mélange. En général, cette courbe est monotone et non-linéaire. Elle est bien souvent exprimée comme une relation quasi-linéaire avec le coefficient
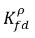
équation 2.204
où la valeur K
f,d est généralement décidée à l'aide de lois physiques ou de corrélations empiriques. Bien souvent, on applique la
loi de Henry, qui fournit une relation généralisée à l'équilibre. Selon cette loi, pour un mélange liquide en contact avec la phase gazeuse, la pression partielle du gaz libre ρ
g,f est égale au produit de la fraction molaire à l'équilibre du gaz dissous dans la phase liquide,
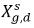
et à la constante de Henry, H
x :
équation 2.205
Si la phase du gaz libre suit la loi des gaz parfaits, la loi de Dalton sur la pression partielle donne l'équation suivante :
équation 2.206
équation 2.207
La constante de Henry inclut donc une unité de pression et peut être considérée comme une pression de référence. Si l'on part du principe que, pour un mélange liquide idéal en contact avec un gaz, la constante de Henry correspond à la pression de la vapeur de saturation p
sat, alors
l'équation 2.207 est également indiquée comme suit :
équation 2.208
où p
d,équil,réf correspond à la pression de référence de la fraction massique à l'équilibre du gaz dissous. Alors,
l'équation 2.204 est réécrite comme suit :
équation 2.209
Dans l'
équation 2.202 et l'
équation 2.203,
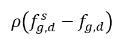
et
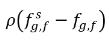
correspondent aux gradients/différences de concentration de masse, et aux forces régissant l'absorption/la dissolution et la libération des gaz non condensables. Cela indique que la concentration de masse ne doit plus être à l'état d'équilibre pour que les gaz non condensables soient transportés sur deux phases. La direction du transfert de masse pousse le système vers l'équilibre en fonction des concentrations de masse à l'équilibre et locales pour les deux phases. D'après le modèle d'équilibre, vous obtenez :
◦ Absorption/dissolution du gaz dans un liquide : le transfert de masse s'effectue de la phase gazeuse (gaz libre) vers la phase liquide (gaz dissous). Le modèle relatif à l'équilibre suppose que le gaz libre à la phase gazeuse est à l'état d'équilibre :
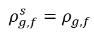
. Si l'on utilise
l'équation 2.204 et
l'équation 2.209, on obtient ce qui suit :
équation 2.210
équation 2.211
équation 2.212
◦ Libération du gaz d'un liquide : le transfert de masse s'effectue de la phase liquide (gaz dissous) vers la phase gazeuse (gaz libre). Lors de ce processus, le modèle relatif à l'équilibre part du principe que le gaz dissous à la phase liquide est toujours à l'état d'équilibre :
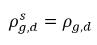
. D'après l'
équation 2.202, l'
équation 2.203, l'
équation 2.204 et l'
équation 2.209, les débits de transfert massique sont les suivants :
équation 2.213
équation 2.214
Notez que lorsqu'une partie des gaz non condensables est dissoute dans le liquide, le gaz librement expansible correspond uniquement à la partie restant à la phase gazeuse, fg,f. Par conséquent, la masse volumique du mélange est calculée comme suit :
équation 2.215
et la fraction volumique du gaz libre est la suivante :
équation 2.216
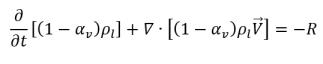
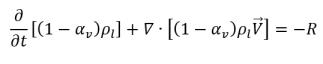
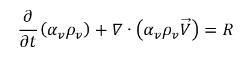
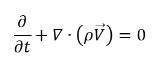
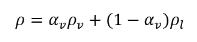
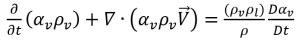
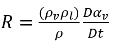
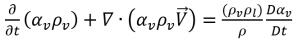
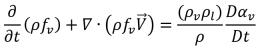
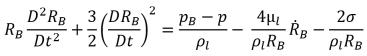
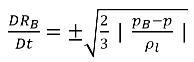
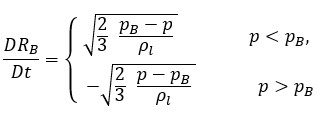
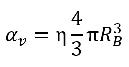
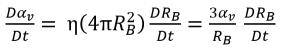
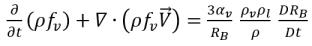
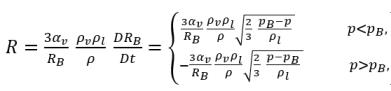
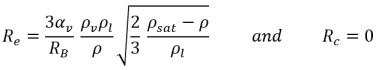
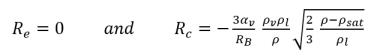
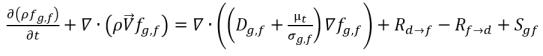
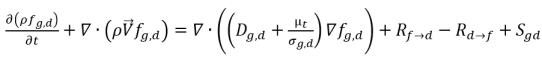
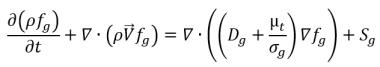
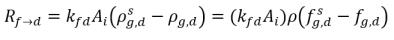
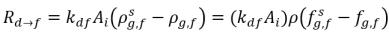
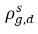
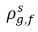
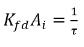 est associé à l'unité de temps inversé (1/s), un indicateur de l'efficacité du transfert de masse. Par conséquent, l'équation 2.200 et l'équation 2.201 ont également les formes suivantes :
est associé à l'unité de temps inversé (1/s), un indicateur de l'efficacité du transfert de masse. Par conséquent, l'équation 2.200 et l'équation 2.201 ont également les formes suivantes :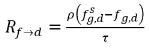
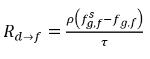
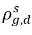 et
et 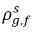 ne sont pas identiques (discontinuité). Il existe une courbe bien définie représentant l'équilibre entre les deux concentrations. Elle dépend de la température, de la pression et des compositions du mélange. En général, cette courbe est monotone et non-linéaire. Elle est bien souvent exprimée comme une relation quasi-linéaire avec le coefficient
ne sont pas identiques (discontinuité). Il existe une courbe bien définie représentant l'équilibre entre les deux concentrations. Elle dépend de la température, de la pression et des compositions du mélange. En général, cette courbe est monotone et non-linéaire. Elle est bien souvent exprimée comme une relation quasi-linéaire avec le coefficient 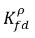
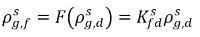
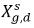 et à la constante de Henry, Hx :
et à la constante de Henry, Hx :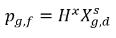
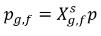
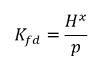
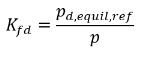
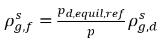
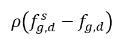 et
et 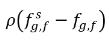 correspondent aux gradients/différences de concentration de masse, et aux forces régissant l'absorption/la dissolution et la libération des gaz non condensables. Cela indique que la concentration de masse ne doit plus être à l'état d'équilibre pour que les gaz non condensables soient transportés sur deux phases. La direction du transfert de masse pousse le système vers l'équilibre en fonction des concentrations de masse à l'équilibre et locales pour les deux phases. D'après le modèle d'équilibre, vous obtenez :
correspondent aux gradients/différences de concentration de masse, et aux forces régissant l'absorption/la dissolution et la libération des gaz non condensables. Cela indique que la concentration de masse ne doit plus être à l'état d'équilibre pour que les gaz non condensables soient transportés sur deux phases. La direction du transfert de masse pousse le système vers l'équilibre en fonction des concentrations de masse à l'équilibre et locales pour les deux phases. D'après le modèle d'équilibre, vous obtenez :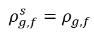 . Si l'on utilise l'équation 2.204 et l'équation 2.209, on obtient ce qui suit :
. Si l'on utilise l'équation 2.204 et l'équation 2.209, on obtient ce qui suit :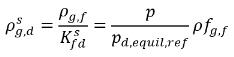
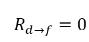
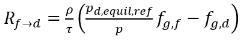
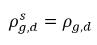 . D'après l'équation 2.202, l'équation 2.203, l'équation 2.204 et l'équation 2.209, les débits de transfert massique sont les suivants :
. D'après l'équation 2.202, l'équation 2.203, l'équation 2.204 et l'équation 2.209, les débits de transfert massique sont les suivants :