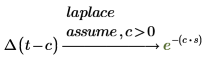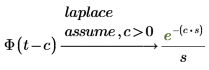Преобразования

Символьные операции > Работа с символьными операциями > дифференциальные и интегральные; > Преобразования

Преобразования

Функция PTC Mathcad, к которой может быть применено ключевое слово преобразования, должна иметь независимую переменную по умолчанию, показанную в таблице ниже, в столбце "Функция" (Function). Если нужно применить для функции другую независимую переменную, необходимо ввести запятую, а за ней - имя переменной. PTC Mathcad возвращает преобразованную функцию, для которой переменная, заданная по умолчанию, находится в столбце "Преобразованная функция" (Transformed Function).

Ключевое слово	Преобразование	Переменные по умолчанию
Ключевое слово	Преобразование	Функция	Преобразованная функция
fourier	Преобразование Фурье	t	ω
invfourier	Обратное преобразование Фурье	ω	t
laplace	Преобразование Лапласа	t	s
invlaplace	Обратное преобразование Лапласа	s	t
ztrans	z-преобразование	n	z
invztrans	Обратное z-преобразование	z	n

• Найдите преобразование Лапласа функции:

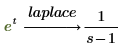
Поскольку независимая переменная t является переменной функции по умолчанию для laplace, имя переменной указывать не нужно. PTC Mathcad возвращает преобразованную функцию с переменной по умолчанию s, как показано в столбце "Преобразованная функция" (Transformed Function) выше.

Если функцией используется другая независимая переменная, например x, необходимо указать эту переменную после laplace.

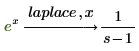
• Если у функции более одной переменной, введите для функции независимую переменную справа от laplace:

<region id="ID0EAEAMB" actualWidth="151.85666666666665" actualHeight="51.158666666666669" top="153.60000000000002" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="12">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <pow />
        <id labels="CONSTANT" label-is-contextual="true" xml:space="preserve">e</id>
        <apply>
          <mult />
          <apply>
            <neg />
            <id xml:space="preserve">a</id>
          </apply>
          <id xml:space="preserve">t</id>
        </apply>
      </apply>
      <command>
        <sequence>
          <id xml:space="preserve">laplace</id>
          <id xml:space="preserve">t</id>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <real>1</real>
          <apply>
            <plus />
            <id labels="*" xml:space="preserve">s</id>
            <id labels="*" xml:space="preserve">a</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

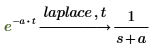
• Переменную по умолчанию для преобразованной функции можно изменить:

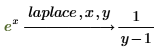
• Переменная по умолчанию для преобразованной функции не может быть использована в качестве независимой переменной для исходной функции:

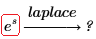
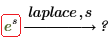
• Для возврата не полностью упрощенных результатов используйте модификатор raw после ключевого слова преобразования. Например, сравните следующие результаты ztrans:

<region id="ID0EGJAMB" actualWidth="214.53333333333333" actualHeight="51.158666666666669" top="384.00000000000006" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="16">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <pow />
          <id xml:space="preserve">x</id>
          <real>2</real>
        </apply>
        <apply>
          <mult />
          <real>3</real>
          <id xml:space="preserve">x</id>
        </apply>
      </apply>
      <command>
        <id xml:space="preserve">ztrans</id>
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <mult />
            <parens>
              <apply>
                <plus />
                <apply>
                  <pow />
                  <id labels="*" xml:space="preserve">x</id>
                  <real>2</real>
                </apply>
                <apply>
                  <mult />
                  <real>3</real>
                  <id labels="*" xml:space="preserve">x</id>
                </apply>
              </apply>
            </parens>
            <id labels="*" xml:space="preserve">z</id>
          </apply>
          <apply>
            <minus />
            <id labels="*" xml:space="preserve">z</id>
            <real>1</real>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

<region id="ID0EUJAMB" actualWidth="401.18333333333334" actualHeight="53.31066666666667" top="460.80000000000007" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="17">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <plus />
        <apply>
          <pow />
          <id xml:space="preserve">x</id>
          <real>2</real>
        </apply>
        <apply>
          <mult />
          <real>3</real>
          <id xml:space="preserve">x</id>
        </apply>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">ztrans</id>
            <id xml:space="preserve">x</id>
          </sequence>
          <id xml:space="preserve">raw</id>
        </sequence>
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <div />
            <apply>
              <mult />
              <real>3</real>
              <id labels="*" xml:space="preserve">z</id>
            </apply>
            <apply>
              <plus />
              <apply>
                <minus />
                <apply>
                  <pow />
                  <id labels="*" xml:space="preserve">z</id>
                  <real>2</real>
                </apply>
                <apply>
                  <mult />
                  <real>2</real>
                  <id labels="*" xml:space="preserve">z</id>
                </apply>
              </apply>
              <real>1</real>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <plus />
              <apply>
                <pow />
                <id labels="*" xml:space="preserve">z</id>
                <real>2</real>
              </apply>
              <id labels="*" xml:space="preserve">z</id>
            </apply>
            <apply>
              <minus />
              <apply>
                <plus />
                <apply>
                  <minus />
                  <apply>
                    <pow />
                    <id labels="*" xml:space="preserve">z</id>
                    <real>3</real>
                  </apply>
                  <apply>
                    <mult />
                    <real>3</real>
                    <apply>
                      <pow />
                      <id labels="*" xml:space="preserve">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
                <apply>
                  <mult />
                  <real>3</real>
                  <id labels="*" xml:space="preserve">z</id>
                </apply>
              </apply>
              <real>1</real>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

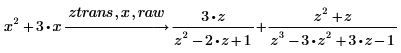
• Чтобы вычислить преобразование Лапласа для кусочных функций, таких как дельта-функция Дирака или функция Хевисайда, в которых присутствуют дополнительные параметры, можно указать знак всех параметров с помощью ключевого слова assume. Например:

<region id="ID0EILAMB" actualWidth="205.50666666666666" actualHeight="57.800000000000004" top="556.80000000000007" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="18">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="FUNCTION" xml:space="preserve">Δ</id>
        <apply>
          <minus />
          <id xml:space="preserve">t</id>
          <id xml:space="preserve">c</id>
        </apply>
      </apply>
      <command>
        <id xml:space="preserve">laplace</id>
      </command>
      <command>
        <sequence>
          <id xml:space="preserve">assume</id>
          <apply>
            <greaterThan />
            <id xml:space="preserve">c</id>
            <real>0</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <pow />
          <id labels="CONSTANT" xml:space="preserve">e</id>
          <apply>
            <neg />
            <parens>
              <apply>
                <mult />
                <id labels="*" xml:space="preserve">c</id>
                <id labels="*" xml:space="preserve">s</id>
              </apply>
            </parens>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Щелкните для копирования этого выражения

<region id="ID0EWLAMB" actualWidth="309.02666666666664" actualHeight="57.800000000000004" top="633.60000000000014" left="0" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="19">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">Φ</id>
        <apply>
          <minus />
          <id xml:space="preserve">t</id>
          <id xml:space="preserve">c</id>
        </apply>
      </apply>
      <command>
        <id xml:space="preserve">laplace</id>
      </command>
      <command>
        <sequence>
          <id xml:space="preserve">assume</id>
          <apply>
            <greaterThan />
            <id xml:space="preserve">c</id>
            <real>0</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <id labels="*" xml:space="preserve">laplace</id>
          <sequence>
            <apply>
              <id labels="FUNCTION" xml:space="preserve">Φ</id>
              <apply>
                <minus />
                <id labels="*" xml:space="preserve">t</id>
                <id labels="*" xml:space="preserve">c</id>
              </apply>
            </apply>
            <id labels="*" xml:space="preserve">t</id>
            <id labels="*" xml:space="preserve">s</id>
          </sequence>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

Похожие темы

Вставка ключевых слов и модификаторов

Пример. Аналитические преобразования

Пример. Пары преобразований

Было ли это полезно?