Многомерная полиномиальная регрессия
• polyfit(X, Y, n/"terms"/M): определяет функцию, описывающую поверхность многомерной полиномиальной регрессии, которая подгоняет результаты, записанные в матрице Y, к данным, найденным в матрицеX. Уравнение полиномиальной регрессии можно определить, задав степень полинома n, а также при помощи его членов, как указано в строке “terms” или в матрице M. Используйте матрицу M, если не требуется включать пересечение в аппроксимацию полиномом.
Рассмотрим, например, функцию полиномиальной регрессии p:
p := polyfit(X, Y ,1)
p(v) = 1.075
Функция p берет векторный аргумент v, указывающий значение для каждой независимой переменной p, как описывается матрицей X. Каждая переменная вектора v должна иметь единицы, совместимые с соответствующим столбцом матрицы X. Единицы измерения, возвращаемые аппроксимирующей функцией p, совместимы с единицами измерения матрицы Y.
Аргументы
• X — матрица плана или матрица, в которой каждый столбец представляет независимую переменную. Каждый столбец X должен иметь совместимые единицы измерения.
• Y — вектор или матрица с результатами измерений или моделирования, где каждая строка содержит результаты отдельного выполнения или точку данных, определенную в X. Если строки содержат неодинаковое число реплик, необходимо заполнить пустые элементы Y значениями NaN. Элементы матрицы Y должны иметь совместимые единицы измерения.
• n — целое число, задающее степень полинома. Оно должно быть меньше общего числа точек данных: 1 ≤ n ≤ length(Y) − 1. В противном случае задача недостаточно ограничена и не имеет уникального решения.
• “terms” — строка, содержащая члены или факторы и взаимодействия, которые требуется включить в полиномиальную регрессию. Строка "A B AB AA BB" означает, что полином содержит следующие члены:
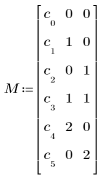
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
В качестве разделителя можно использовать пробел, запятую, двоеточие или точку с запятой.
• M — матрица, задающая полином, с начальными значениями коэффициентов в первом столбце и показателями степени независимых переменных для каждого члена в остальных столбцах. Для описанного выше полинома определите матрицу M следующим образом.
Дополнительная информация
В разделе Устаревшие функции рекомендуется использовать функцию polyfit в качестве альтернативы устаревшей функции regress.
Вывод функции regress представляет собой матрицу коэффициентов, которая передается в функцию interp для получения аппроксимирующей функции.
Выходные данные функции polyfit представляют собой аппроксимирующую функцию, поэтому не требуется вызывать функцию interp.