Пример. Преобразование Гильберта
Функция hilbert используется для создания такого преобразования Гильберта вещественного сигнала, чтобы дискретное преобразование Фурье аналитического сигнала имело нулевую величину на отрицательных частотах.
1. Используйте функции sin и cos для определения входного сигнала. Используйте функцию rnd для добавления случайного шума.
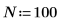
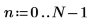
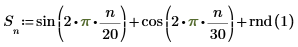
2. Постройте график входного сигнала.
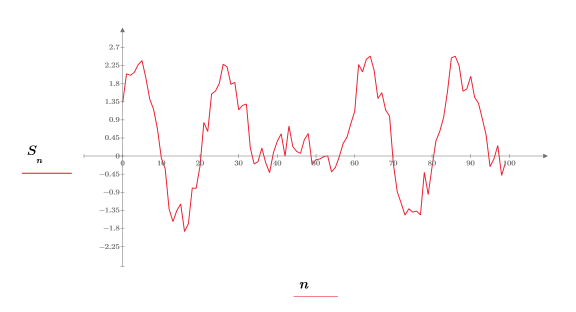
3. Используйте функцию hilbert, чтобы вычислить преобразование Гильберта входного сигнала.
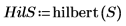
4. Постройте график сигнала преобразования Гильберта.
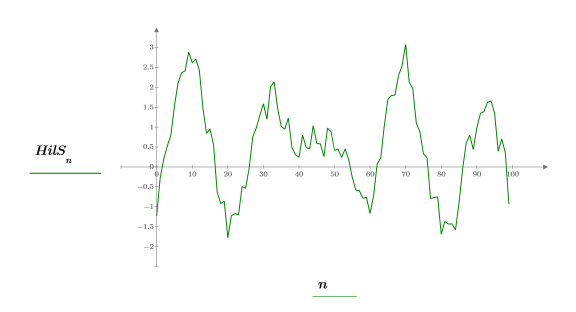
5. Скомпонуйте и постройте график комплексного сигнала.
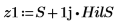
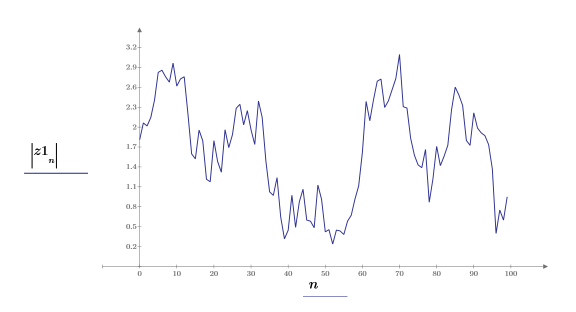
В следующих шагах будет показано, что величина аналитического сигнала представляет собой комплексную огибающую исходного сигнала.
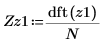
7. Постройте график абсолютных значений спектра.
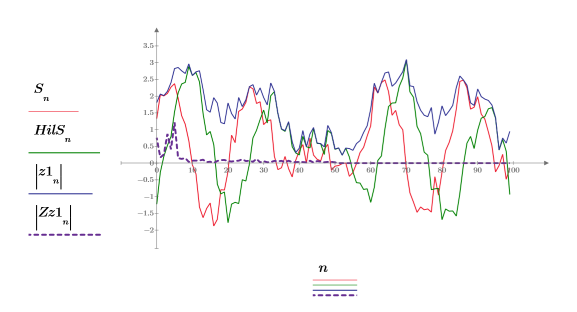
Для векторов коэффициент масштабирования между функцией dft и устаревшей функцией CFFT равен 1/N.
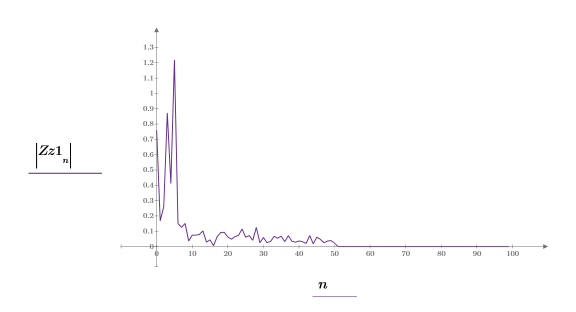
8. Постройте общий график всех четырех сигналов.
Новый сигнал, создаваемый преобразованием Гильберта, связан с входным сигналом в области преобразования следующим образом:
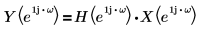
где H - преобразователь Гильберта, фильтр с частотной характеристикой:
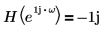 | для | 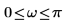 | |
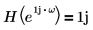 | для | 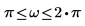 |
Существует возможность провести компоновку H через процедуры и функции конструирования фильтра.
Идеальный преобразователь Гильберта
Коэффициенты для идеального преобразователя Гильберта представлены в книге Lawrence R. Rabiner and Bernard Gold. Theory and Application of Digital Signal Processing, Prentice-Hall, Inc. Дальнейшие примеры основаны на трактовке, приведенной в разделе 14.4 книги Samuel Stearns and Ruth David. Signal Processing Algorithms (Prentice-Hall). Коэффициенты идеального фильтра кадрируются и сдвигаются для получения причинного фильтра нечетной длины L.
1. Задайте длину и центр.
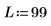
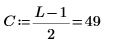
2. Задайте некадрированные коэффициенты h.
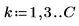 | ||
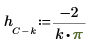 | 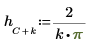 | 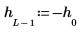 |
3. Используйте функцию hamming, чтобы кадрировать коэффициенты с помощью окна Хэмминга, применяя оператор vectorize для перемножения h и окна, элемент за элементом.
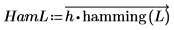
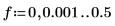
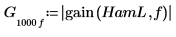
5. Постройте график усиления в зависимости о частоты.
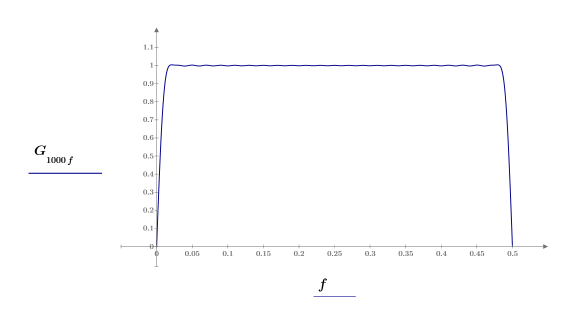
Частота нормализуется до частоты выборки 1.
Фильтр имеет задержку в C, и мы вычисляем фазовый сдвиг фильтра, связанный с задержанным сигналом. Задержка обладает следующей передаточной функцией:
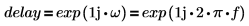 | ||
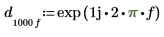 | ||
где: | 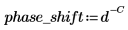 | |
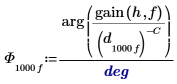 | ||
7. Постройте график фазового сдвига в градусах.
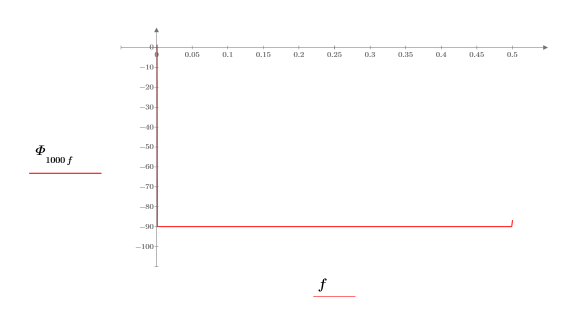
Сдвиг равен -90 градусов почти по всему частотному диапазону.
Испытание фильтра
1. Определите параметры сигнала.
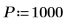
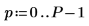
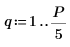
2. Используйте функцию exp для создания нового сигнала. Функция rnd добавляет низкочастотный шум.
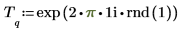
Если навести курсор на rnd и нажать клавишу F5 для пересчета, можно увидеть другой случайный сигнал T.
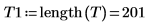
3. Поместите сопряжения этих элементов в последние 200 расположений сигнала, чтобы обеспечить вещественный результат при инвертировании.
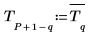
Новый вектор имеет 1001 элемент, где элементы 1-200 содержат исходный вектор T, а элементы 801-1000 содержат сопряжения T. Для промежуточных элементов установлено значение 0.
4. Найдите преобразование Фурье сигнала T.
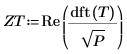
Используйте функцию Re для удаления небольшой мнимой ошибки округления. Шум генерируется путем построения для него преобразования T с использованием случайных фаз и величин единиц для первых 200 элементов после первого.
5. Постройте график преобразованного сигнала.
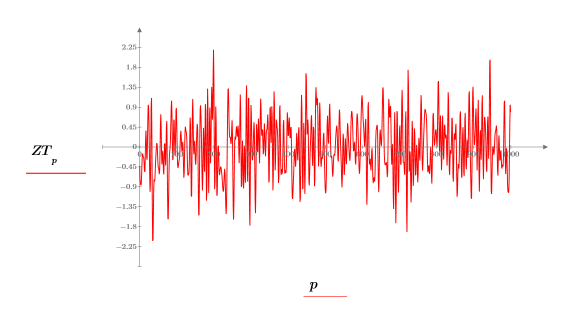
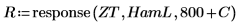
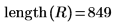
7. Скомпонуйте комплексный сигнал z2, используя первые 800 элементов ZT и последние 800 элементов R.
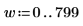
Сохраните первые 800 элементов вектора преобразования Фурье ZT в вектор a2.
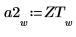
Сохраните последние 800 элементов вектора отклика R в вектор b2.
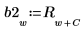
Определите комплексный сигнал z2.
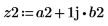
8. Используйте функцию dft, чтобы вычислить дискретное преобразование Фурье сигнала z2.
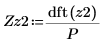
Для векторов коэффициент масштабирования между функцией dft и устаревшей функцией CFFT равен 1/P.
9. Постройте график абсолютных значений дискретного преобразования Фурье сигнала z2.
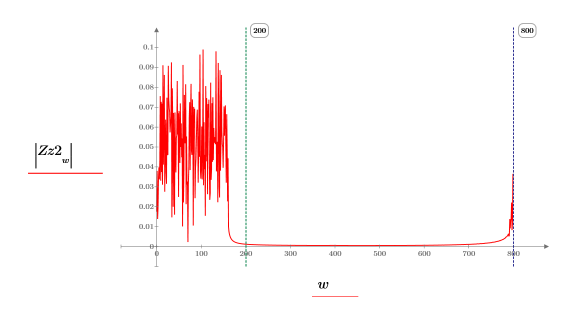
Исходные 200 точек, использовавшиеся для создания сигнала в области преобразования, показаны здесь. Верхняя половина спектра, в сущности, равна нулю, так что фильтр преобразователя Гильберта свою работу выполнил.