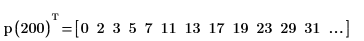Пример. Рекурсивные функции
Используйте возможности программирования PTC Mathcad, чтобы определить рекурсивные функции.
Пример 1. Определение факториала
1. Определите функцию Fac, которая вычисляет факториал n. Пометьте функцию с помощью метки "Функция" (Function).
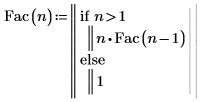
2. Рассчитайте значение факториала 6 с помощью функции Fac и проверьте его с помощью оператора факториала PTC Mathcad.
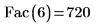
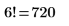
3. Определите другую функцию Fac с другим условием для n и вызовите функцию, как показано ниже.
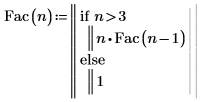
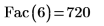
PTC Mathcad выдает тот же результат, поскольку возвращается к предыдущему определению Fac для выполнения расчета.
4. Отключите первое определение функции Fac, чтобы увидеть различие в результатах. Во избежание такой неоднозначности не используйте имена функций повторно.
Пример 2. Расчет наибольшего общего делителя двух положительных целых чисел
1. Запишите рекурсивную функцию GCD, которая рассчитывает наибольший общий делитель двух чисел, т. е. наибольшее целое число, на которое без остатка делятся x и y.
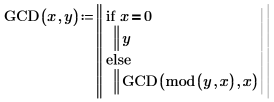
2. Вызовите эту функцию с разными значениями.
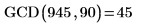 | 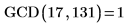 |
Эта программа совпадает со встроенной функцией наибольшего общего делителя gcd:
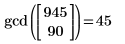 | 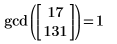 |
Пример 3. Определение n-й итерации функции f(x) в точке a
1. Запишите вложение рекурсивной функции, которое рассчитывает n-ю итерацию функции f(x) в точке a.
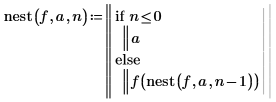
2. Задайте функцию f(x) и назначьте значение 1 для a.
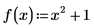
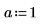
3. Вызовите эту функцию с разными значениями.
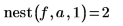 | 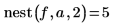 |
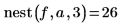 | 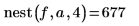 |
Пример 4. Задание последовательности Фибоначчи (два рекурсивных вызова на инициирование)
1. Запишите функцию fib, которая рассчитывает значение последовательности чисел Фибоначчи для n.
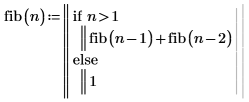
2. Задайте вектор k и вызовите функцию fib.
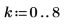

Пример 5. Определение функции разбиения
1. Запишите рекурсивную функцию part, которая рассчитывает количество различных способов выразить m как сумму положительных целых чисел, не превышающих n.

2. Вызовите эту функцию с разными значениями.
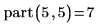
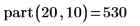
Пример 6. Создание случайного бинарного дерева
1. Напишите рекурсивную функцию Tree, которая создает случайное бинарное дерево.
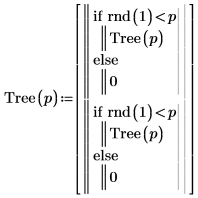
2. Вызовите функцию.

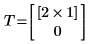
Пример 7. Поиск высоты бинарного дерева
1. Напишите рекурсивную функцию height, которая возвращает высоту бинарного дерева.
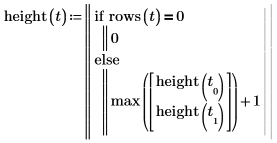
2. Вызовите функцию для дерева, созданного в предыдущем примере.
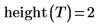
Так как Tree создает случайное бинарное дерево, возвращаемая высота изменяется после каждого повторного вычисления. |
Пример 8. Настройка решета Эратосфена для поиска простых чисел
1. Используйте функцию ceil, чтобы записать рекурсивную функцию p, которая находит все простые числа меньше n, используя решето Эратосфена.

2. Вызовите функцию, чтобы получить вектор всех простых чисел меньше 200.