Пример. Распределения вероятностей
Используйте функции распределения вероятностей вместо таблиц распределения вероятностей.
Плотность вероятности
1. Используйте функцию dchisq, чтобы вычислить плотность вероятности переменной с распределением хи-квадрат с 11 степенями свободы для значения 5.5:
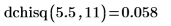
2. Используйте функцию dt, чтобы вычислить плотность вероятности переменной t с распределением хи-квадрат с 4 степенями свободы для значения -1.56:
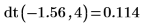
Кумулятивная вероятность
1. Используйте функцию pnorm, чтобы вычислить вероятность того, что стандартная нормальная переменная превышает 1.0:
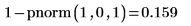
2. Используйте функцию pchisq, чтобы вычислить вероятность того, что переменная с распределением хи-квадрат с 7 степенями свободы меньше 5.6:
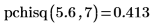
3. Используйте функцию pbinom, чтобы вычислить вероятность того, что переменная с биномиальным распределением с 15 степенями свободы и параметром 0.6 меньше либо равна 10.
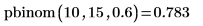
4. Используйте функцию qbinom, чтобы вычислить вероятность того, что переменная с биномиальным распределением с 15 степенями свободы и параметром 0.6 меньше либо равна 10.
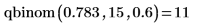
5. Используйте функцию rbinom, чтобы создать вектор из m=5 случайных чисел, имеющих биномиальное распределение с размером n=7 и вероятностью успешного исхода q=0.65.
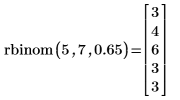
Пересчет документа приводит к тому, что функция rbinom возвращает новый набор случайных чисел. |
6. Используйте функцию dbeta, чтобы вычислить плотность вероятности для значения x=0.8 при действительных параметрах формы 3 и 2:
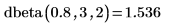
7. Используйте функцию pbeta, чтобы вычислить вероятность того, что переменная beta при a=3 и b=2 превышает 0.8:
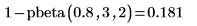
8. Используйте функцию qbeta, чтобы вычислить обратное кумулятивное распределение вероятностей для вероятности p=0.8:
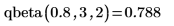
9. Используйте функцию rbeta, чтобы создать вектор из m=5 случайных чисел, имеющих биномиальное распределение с размером n=6 и вероятностью успешного исхода q=0.75.
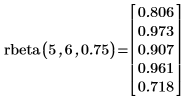
Обратная кумулятивная вероятность
1. Используйте функцию qnorm, чтобы вычислить обратное кумулятивное распределение вероятностей для вероятности p:
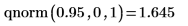
2. Используйте функцию qt, чтобы вычислить обратное кумулятивное распределение вероятностей для вероятности p:
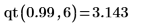
Распределение Фишера
1. Используйте функцию dF, чтобы вычислить 65-й процентиль для распределения Фишера с 4 и 6 степенями свободы:
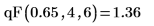
2. Используйте функцию pF, чтобы вычислить кумулятивное распределение вероятностей для вероятности 0.75 с 5 и 7 степенями свободы:
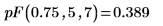
3. Используйте функцию qF, чтобы вычислить 95%-й процентиль для распределения Фишера с 9 и 8 степенями свободы:
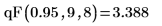
4. Используйте функцию rF, чтобы создать вектор из 7 случайных чисел, имеющих распределение Фишера с 3 степенями свободы:

Пересчет документа приводит к тому, что функция rF возвращает новый набор случайных чисел. |