Пример. Обратное преобразование idft
Функция idft является обратным преобразованием функции dft, а потому должна восстанавливать исходные входные данные до комплексного преобразования.
Работа с векторами (1D)
1. Определите длину вектора v.
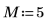
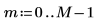
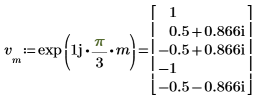
3. Используйте функцию dft для вычисления прямого преобразования вектора v.
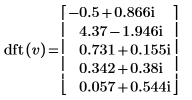
4. Используйте функцию idft для вычисления обратного преобразования вектора v.

5. Покажите, что обратное преобразование прямого преобразования вектора v является исходным вектором v.
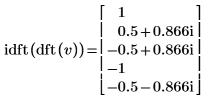 |  |
Результаты идентичны.
Работа с матрицами (2D)
1. Определите и вычислите матрицу C.
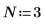
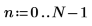
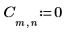
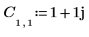
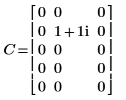
2. Используйте функцию dft для вычисления прямого преобразования матрицы C.

3. Используйте функцию idft для вычисления обратного преобразования матрицы C.

4. Покажите, что обратное преобразование прямого преобразования матрицы C является исходной матрицей C.
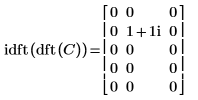 | 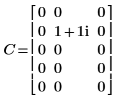 |
Результаты идентичны.
Демонстрация базовой суммы в основе idft
Одномерный случай:
1. Используйте функцию exp и оператор суммы, чтобы вычислить обратное преобразование вектора v.
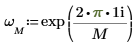
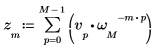
2. Сравните результирующее прямое преобразование вектора v с выходными данными функции dft.
 | 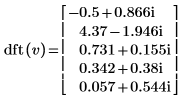 |
Результаты идентичны.
3. Используйте оператор суммы для вычисления обратного преобразования вектора v.
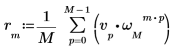
4. Сравните результирующее обратное преобразование вектора v с выходными данными функции idft.
 |  |
Результаты идентичны.
Двухмерный случай:
1. Используйте функцию exp и оператор суммы, чтобы вычислить прямое преобразование матрицы C.
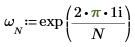
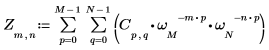
2. Сравните результирующее прямое преобразование матрицы C с выходными данными функции dft.


Результаты идентичны.
3. Используйте оператор суммы для вычисления обратного преобразования матрицы C.
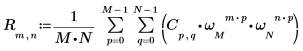
4. Сравните результирующее обратное преобразование матрицы C с выходными данными функции idft.


Результаты идентичны.