Пример. Затухающее гармоническое колебание в электрической цепи
Возьмем простую электрическую схему, содержащую резистор R, катушку L и конденсатор C.
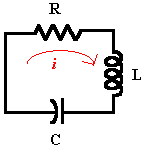
Используйте дифференциальные уравнения для моделирования заряда Q на конденсаторе C, затем используйте функции решателя ОДУ, чтобы найти другие приближенные решения. Наконец, сравните результаты с точным решением Q.
Использование дифференциальных уравнений
1. Запишите дифференциальное уравнение для напряжения на всех трех компонентах, которое в сумме должно равняться нулю:
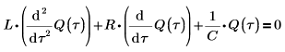
2. Запишите дифференциальное уравнение для мгновенного значения заряда Q в конденсаторе C:
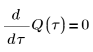
3. Задайте значение заряда Q в нулевой момент времени:
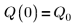
4. Задайте значения следующим входным параметрам:
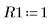
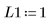
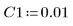
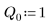
5. Приведите дифференциальное уравнение к стандартной форме:
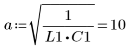
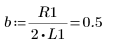
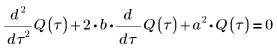
6. Решите уравнение для всех случаев a и b:
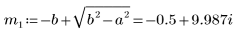
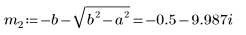
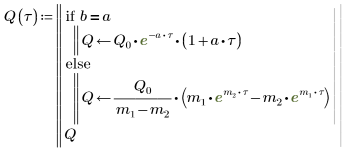
7. Постройте графики двух возможных для Q решений:
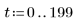
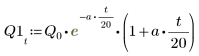
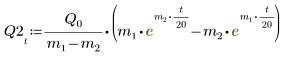
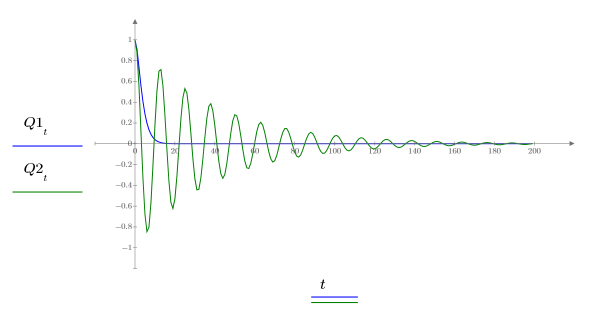
Заряд Q1 быстро уменьшается до нуля, когда a=b, и претерпевает долгие затухающие колебания, когда a не равно b.
Действия перед использованием решателей ОДУ
• Задайте параметры для передачи в функции решателя ОДУ:
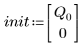 | 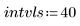 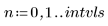 |
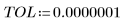 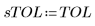 | 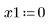 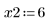 |
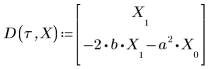 |
• Решатели ОДУ делятся на два типа: решатели для жестких систем и решатели для нежестких систем. Система ОДУ, записанная в матричной форме в виде y' = Ax, называется жесткой, если матрица A является почти сингулярной. В противном случае система считается нежесткой.
• Различие между жесткими и нежесткими системами может быть связано с масштабами динамики, присущей матрице A, которая характеризуется ее собственными значениями. Матрица, имеющая сильно различающиеся собственные значения (или значения, лежащие в диапазоне от очень малых до очень больших) обычно представляет жесткую систему.
• С указанными значениями параметров системы этот простой пример затухающего колебания представляет нежесткую систему.
• В функции Adams, AdamsBDF, BDF и Radau может быть передано конкретное значение TOL или в них будет использоваться их собственное значение TOL по умолчанию 10-5.
Использование решателей ОДУ для нежестких систем
Используя решатели ОДУ для нежестких систем, найдите приближенные решения и сравните результаты с точным решением для Q.
1. Adams
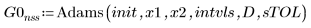
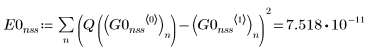
2. rkfixed
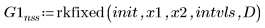
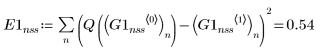
3. Rkadapt
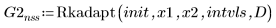
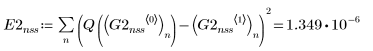
4. Bulstoer
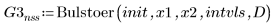
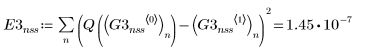
Использование решателей ОДУ для жестких систем
Используя решатели ОДУ для жестких систем, найдите приближенные решения и сравните результаты с точным решением для Q.
1. BDF
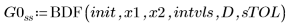
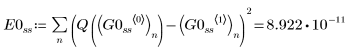
2. Radau
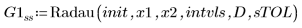
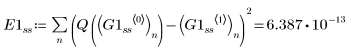
Использование гибридного решателя ОДУ
Используя гибридный решатель ОДУ AdamsBDF, который определяет, является система жесткой или нет, и вызывает, соответственно, решатель Adams или BDF, найдите приближенные решения и сравните результаты с точным решением для Q.
1. AdamsBDF
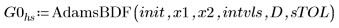
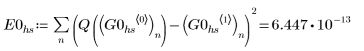
Заключение
• В решателях ОДУ для нежестких систем функции Adams и rkfixed возвращают решения с наименьшей и наибольшей погрешностью, соответственно.
• В решателях ОДУ для жестких систем функции Radau и BDF возвращают решения с меньшей и большей погрешностью, соответственно.
• Гибридная функция AdamsBDF возвращает значение меньшее, чем оба значения, возвращаемые функциями Adams или BDF.
• Наконец, функции Radau и rkfixed возвращают решения с наименьшей и наибольшей погрешностью, соответственно.
Сравнение результатов
1. Постройте графики решений, найденных решателями ОДУ для нежестких систем с наименьшей (Adams, G0nss) и наибольшей (rkfixed, G1nss) погрешностями:
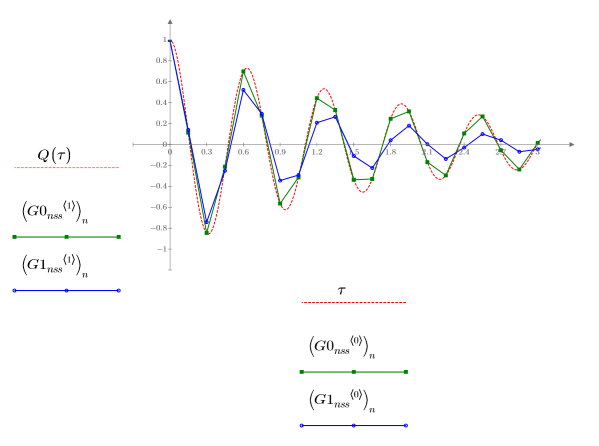
Между двумя полученными решениями есть заметная разница, если сравнивать с Q.
2. Постройте графики решений, найденных решателями ОДУ для жестких систем с наименьшей (Radau, G1ss) и наибольшей (BDF, G0ss) погрешностями:
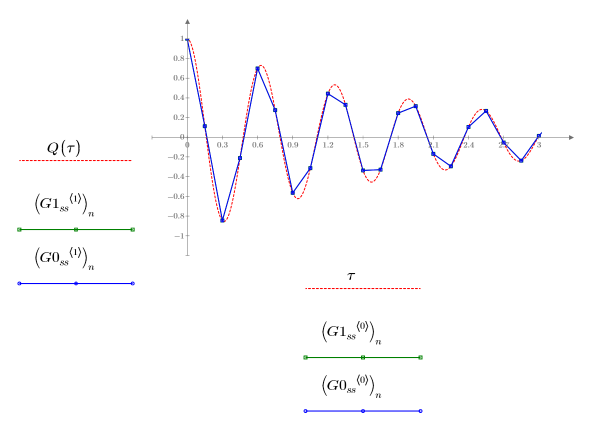
Оба решения совпадают по отношению к Q.
3. Постройте графики решений, дающих наименьшую (Radau, G1ss) и наибольшую (rkfixed, G1nss) погрешности, возвращаемые решателями ОДУ для жестких и нежестких систем:
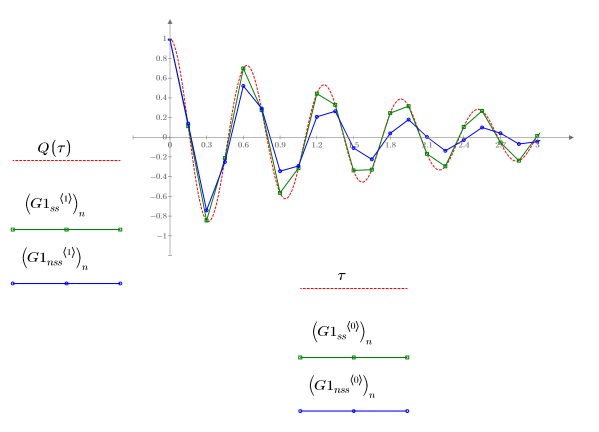
Функция Radau, решатель для жесткой системы, возвращает наилучшую аппроксимацию решения для Q.