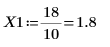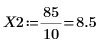Пример. Функции Бесселя первого рода
Покажите взаимосвязь между функциями J0, J1 и Jn. Также покажите взаимосвязи между этими функциями и их масштабированными версиями.
1. Определите две переменные определения шага:
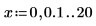
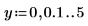
2. Постройте графики функций J0 и J1. Добавьте функцию 2-го порядка Jn на график:
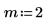
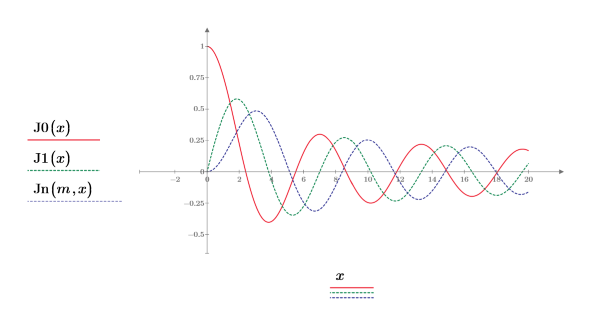
3. Создайте график, чтобы показать, что J0(y)=Jn(0,y). Сбросьте значения делений, чтобы увеличить масштаб по оси X и показать график более подробно:
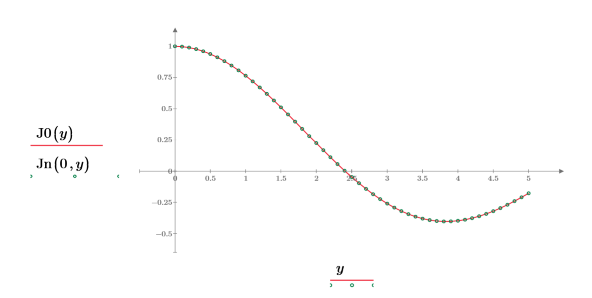
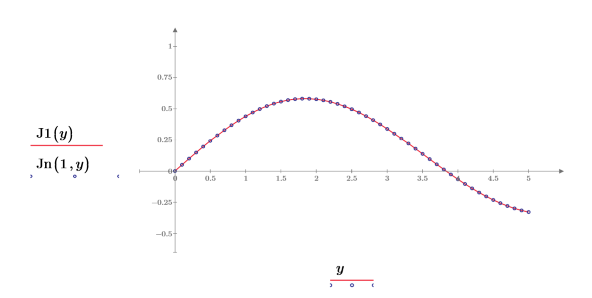
4. Создайте график, чтобы показать, что J1(y)=Jn(1,y). Сбросьте значения делений, чтобы увеличить масштаб по оси X и показать график более подробно:
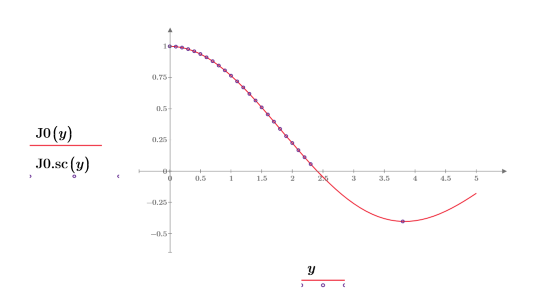
5. Используйте аналитические преобразования, чтобы показать взаимосвязь между каждой функцией Бесселя первого рода и ее масштабированной версией:
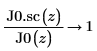
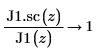
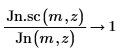
6. Создайте график, чтобы показать, что:
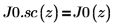
J0.sc содержит комплексные элементы, поэтому сначала примените функцию Re, чтобы просто показать вещественную часть чисел.
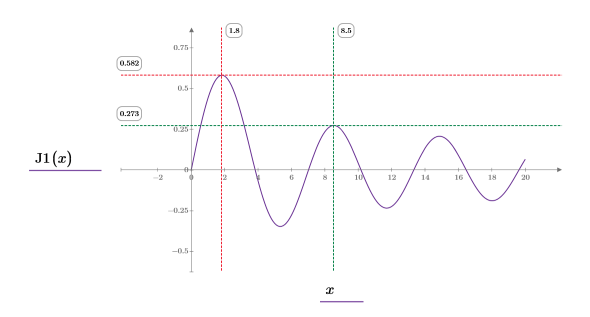
7. Вычислите координаты первых двух пиков J1. Используйте функции augment и localmax, чтобы идентифицировать пики, попадающие в указанный диапазон:
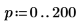
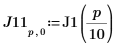
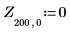
Для функции localmax требуется входная матрица с двумя столбцами. Функция augment используется для создания такой матрицы.
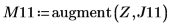

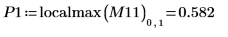
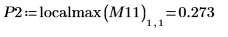
8. Используйте функцию match, чтобы найти координаты пиков по горизонтали. Уменьшите значение TOL, чтобы получить более точные результаты:
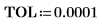
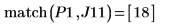
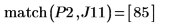
9. Добавьте маркеры на график, чтобы отметить первые два пика:
Переменная определения шага имеет шаг 0.1. Это означает, что пики возникают на 1/10 индекса элемента, который определяется функцией match или 1.8 и 8.5 соответственно.