Вычисление функций аналитически
При вычислении функции с использованием оператора аналитического преобразования PTC Mathcad выполняет подстановку аргумента в функцию и вычисляет ее аналитически.
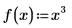
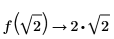
В качестве аргумента функции можно использовать символическое выражение следующим образом:
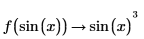
Вычислять аналитически можно также стандартные операторы PTC Mathcad и многие встроенные функции, включая большинство обычных числовых функций, таких как sin(x) и ex.
Чтобы применить функцию к вектору и вычислить ее значение аналитически, воспользуйтесь оператором умножения векторов. Например, чтобы вычислить значение косинуса для каждого элемента следующего вектора, примените оператор умножения векторов к функции cos(v) следующим образом:
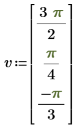 | 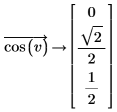 |
Некоторые встроенные функции сохраняют свое обычное значение в аналитических вычислениях, но многие из них теряют смысл в аналитическом контексте и не вычисляются. Некоторые из этих функций при аналитических преобразованиях имеют другое значение или имеют ограничения:
• В отличие от числовой функции mod, аналитической функции mod требуется целочисленный модуль и она может получать полином в качестве первого аргумента.
• Некоторые аналитические обратные тригонометрические функции используют разные ветви комплексной плоскости.
• С помощью функции eigenvals можно аналитически вычислить значения для комплексных и вещественных матриц.