Regresión polinomial multivariada
• polyfit(X, Y, n/"terms"/M): define una función que describe una superficie de regresión polinomial multivariada que ajusta los resultados registrados en la matriz Y a los datos encontrados en la matriz X. La ecuación de regresión polinomial se puede definir de acuerdo con su orden polinomial n o con sus términos según se han especificado en la cadena “terms” o en la matriz M. Utilice la matriz M si no desea incluir la intercept en el ajuste polinomial.
Por ejemplo, considere la función de regresión polinomial p:
p := polyfit(X, Y ,1)
p(v) = 1.075
La función p toma un argumento de vector v que especifica un valor de cada variable independiente de p, tal como se describe en la matriz X. Cada variable en el vector v debe tener unidades compatibles con la columna correspondiente de la matriz X. Las unidades devueltas por la función de ajuste p son compatibles con las unidades de la matriz Y.
Argumentos
• X es una matriz de diseño o una matriz en la que cada columna representa una variable independiente. Cada columna de X debe tener unidades compatibles.
• Y es un vector o una matriz de resultados medidos o simulados en que cada fila contiene el resultado de cada ejecución o el punto de datos definido en X. Si las filas no contienen el mismo número de réplicas, rellene los elementos vacíos de Y con NaN. Los elementos de la matriz Y deben tener unidades compatibles.
• n es un número entero que especifica el orden polinomial. Debe ser inferior al número total de puntos de datos: 1 ≤ n ≤ length(Y) − 1. En caso contrario, el problema estará restringido, pero no tendrá una solución única.
• “terms” es una cadena que especifica los términos, o los factores e interacciones, que se deben incluir en la regresión polinomial. "A B AB AA BB" significa que el polinomio contiene los siguientes términos:
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
Para los separadores, se puede usar un espacio, una coma, dos puntos o un punto y coma.
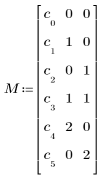
• M es una matriz que especifica un polinomio con valores de prueba para los coeficientes en la primera columna y la potencia de las variables independientes para cada término en las columnas restantes. Con respecto al polinomio descrito anteriormente, defina M como sigue:
Información adicional
El tema Funciones obsoletas recomienda el uso de la función polyfit como alternativa a la función obsoleta regress.
La salida de la función regress es una matriz de coeficientes que se transfiere a la función interp con el fin de obtener la función de ajuste.
La salida de la función polyfit es, en sí misma, una función de ajuste y, por lo tanto, no es necesario llamar a la función interp.