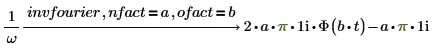Ejemplo: transformadas simbólicas
Realice las transformadas simbólicas de Fourier, Laplace y z, así como sus inversas.
Transformadas de Fourier e inversa de Fourier
1. Utilice la palabra clave fourier para buscar la transformada de Fourier de la función delta de Dirac Δ.
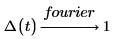
Tal como se esperaba, se devuelve una frecuencia constante.
2. Busque la transformada de Fourier de una función que implique la función escalón de Heaviside Φ.
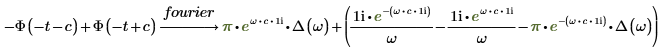
3. Añada la palabra clave simplify para simplificar el resultado.
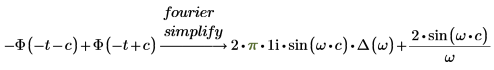
Transformadas de Z e inversa de Z
1. Utilice la palabra clave ztrans para calcular la transformada de z de las dos funciones siguientes:
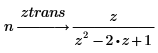
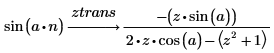
2. Utilice la palabra clave invztrans para calcular la transformada inversa de z de las dos funciones siguientes:
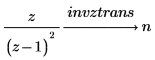
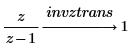
Cambio de la variable por defecto de una transformada
1. Busque la transformada inversa de Laplace de una función
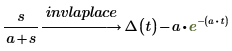
2. Cambie la variable por defecto, t, en la función que devuelve la transformada inversa de Laplace mediante la adición de un par de argumentos después de la palabra clave de la transformada.
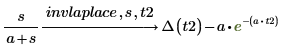
◦ El primer argumento, s, es la variable independiente de la función de dominio.
◦ El segundo argumento, t2, es la nueva variable independiente de la función transformada.
◦ La transformada inversa de Laplace devuelta utiliza la variable t2 como la variable independiente. Δ es la función delta de Dirac.
◦ Δ no se puede evaluar con el signo igual numérico, pero sí con el operador de evaluación simbólica.
3. Busque la transformada de Laplace del resultado mediante la palabra clave laplace.
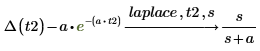
Utilización de más de una palabra clave al mismo tiempo
Si los resultados de un cálculo simbólico no se encuentran en el formato deseado, puede añadir una palabra clave después de la palabra clave de la transformada para modificar el formato del resultado.
1. Busque la transformada de z de una función.
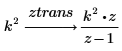
2. Utilice la palabra clave expand para expandir el resultado.
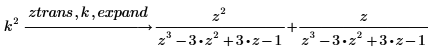
3. Utilice la palabra clave laplace para buscar la transformada de Laplace de una función.
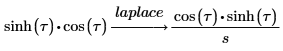
4. Utilice la palabra clave simplify para obtener el resultado en forma simplificada.
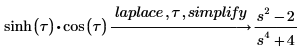
5. Busque las transformadas inversas de Fourier de las funciones sin y sinc, y presente los resultados en forma simplificada.
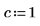
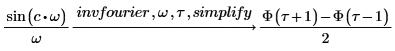
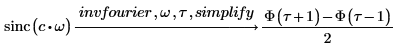
Para las funciones de entrada que carezcan de transformada simbólica, use la función numérica dft.
Factorización de la transformada de Fourier
1. Añada nfact y ofact junto con fourier a la expresión.
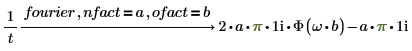
2. Añada nfact y ofact junto con invfourier a la expresión.