Transformada de Fourier discreta de datos
• dft(A), idft(Z): permite devolver la transformada de Fourier directa/inversa de una matriz o un vector de valores complejos.
Si la entrada de dft es un vector V de longitud r, entonces:
◦ La salida de dft(V) es un vector Z de longitud r
◦ La salida de idft(Z) es un vector de longitud r
Si la entrada de dft es una matriz M con r filas y c columnas, entonces:
◦ La salida de dft(M) es una matriz P de r filas y c columnas
◦ La salida de idft(P) es una matriz de r filas y c columnas
• dftr(B), idftr(Z): permite devolver la transformada de Fourier directa/inversa de una matriz o un vector de valores reales.
Si la entrada de dftr es un vector V de longitud r, entonces:
◦ La salida de dftr(V) es un vector Z de longitud L, donde L=floor(r/2)+1. Los elementos de Z son idénticos a los primeros L elementos de la salida de dft(V).
◦ La salida de idftr(Z) es un vector de longitud r=2(L-1).
Si la entrada de dftr es una matriz M con r filas y c columnas, entonces:
◦ La salida de dftr(M) es una matriz P con r filas y L columnas, donde L=floor(c/2)+1. Los elementos de P son idénticos a las primeras L columnas de la salida de dft(M).
◦ La salida de idftr(P) es una matriz de r filas y c=2(L-1) columnas
Argumentos
• A es una matriz o un vector de valores complejos de cualquier tamaño
• B es una matriz o un vector de valores reales. Se desestima cualquier parte imaginaria. Si B es un vector, entonces el número de filas debe ser un múltiplo de 2. Si B es una matriz, entonces el número de columnas debe ser un múltiplo de 2.
• Tanto para A como para B, los datos deben tener unidades compatibles.
Transformada de Fourier de vectores
• Si A es un vector de tamaño m, el elemento número u de la transformada directa unidimensional (1D) del vector A lo da Zu de la siguiente manera:
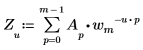
Donde:
◦ m es el número de filas, y u se define como  .
.
 .
.◦ i es la unidad imaginaria y wm se define como:
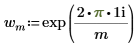
La evaluación de Z en la definición anterior es equivalente a aplicar la función dft al vector A.
• Si Z es un vector de tamaño m, el elemento número u de la transformada inversa unidimensional (1D) del vector Z lo da Au de la siguiente manera:
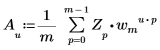
Donde:
◦ m, u y wm se definen anteriormente.
La evaluación de A en la definición anterior es equivalente a aplicar la función idft al vector Z.
Transformada de Fourier de matrices
• Si A es una matriz de tamaño mxn, el elemento número (u,v) de la transformada directa bidimensional (2D) de la matriz A lo da Zu,v de la siguiente manera:

Donde:
◦ m, u y wm se definen anteriormente.
◦ n es el número de columnas, y v se define como: 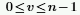 .
.
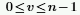 .
.◦ i es la unidad imaginaria y wn se define como:
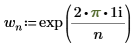
La evaluación de Z en la definición anterior es equivalente a aplicar la función dft a la matriz A.
• Si Z es una matriz de tamaño mxn, el elemento número (u,v) de la transformada inversa bidimensional (2D) de la matriz A lo da Au,v de la siguiente manera:
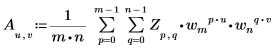
Donde:
◦ m, n, u, v, wm y wn se definen anteriormente.
La evaluación de A en la definición anterior es equivalente a aplicar la función idft a la matriz Z.
Información adicional
• Las funciones de Fourier se ejecutan con mayor rapidez si el número de filas de vectores y de columnas de matrices es una potencia de 2.
• Las nuevas funciones dft/idft reemplazan la funcionalidad de las funciones obsoletas cfft/icfft y CFFT/ICFFT y ofrecen una mejora significativa en el rendimiento, especialmente para los conjuntos de datos más grandes y los casos en que el tamaño no es una potencia de 2.
• Las nuevas funciones dftr/idftr reemplazan la funcionalidad de las funciones obsoletas fft/ifft y FFT/IFFT.
La función dftr opera en vectores reales cuya longitud es un número par y en matrices con un número par de columnas.
• Las funciones fft/FFT solo operan en vectores reales cuya longitud es una potencia de 2.
• Las funciones ifft/IFFT solo tienenla mitad de la longitud del vector de entrada más uno, o 2k-1+1, en que "k" es un entero > 1. La otra mitad, que es el conjugado de la primera parte con el orden invertido, debe reconstruirse manualmente. Las funciones dft/idft devuelven el resultado completo de nuevo.
• Las funciones dft/idft difieren de las funciones desfasadas fft/ifft, FFT/IFFT y cfft/icfft, CFFT/ICFFT tanto en el factor de escala como en el signo del exponente.
◦ Para las transformadas directas, las diferencias son las siguientes:
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
Factor de escala | 1 | 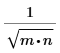 | 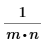 |
Signo del exponente | Negativo | Positivo | Negativo |
◦ Para las transformadas inversas, las diferencias son las siguientes:
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
Factor de escala | 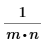 | 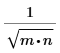 | 1 |
Signo del exponente | Positivo | Negativo | Positivo |
Al calcular el factor de escala de las funciones que operan solo en vectores (casos 1D), se supone que n=1.