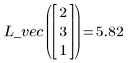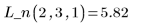Ejemplo: ajuste cuadrático por tramos
Regresión polinomial de una variable
Utilice la función loess para ajustar una serie de funciones cuadráticas a los datos mediante la regresión local.
1. Defina la siguiente matriz:

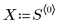
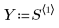
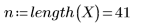
2. Defina el tramo (porcentaje del número total de puntos en una ventana ponderada alrededor de cada punto de datos, que se utiliza para los sucesivos ajustes cuadráticos con la función loess).
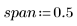
La pauta general es que (span*n ∙ ) debe ser >1, pues es recomendable que la media de puntos mayores que 1 se incluya en cada ajuste ponderado de mínimos cuadrados:
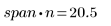
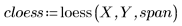
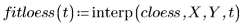
4. Llame a la función polyfit para ajustar un polinomio de segundo orden en el conjunto de datos.
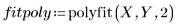
5. Trace las dos curvas definidas arriba.
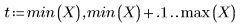
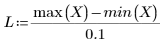
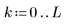
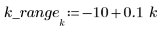
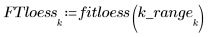
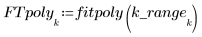
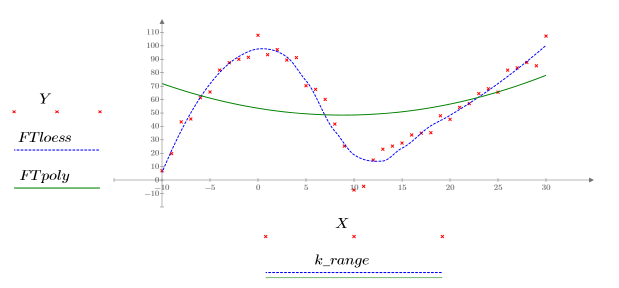
• Si el tramo es grande (por ejemplo, 2 o 3), los datos se consideran como un solo ajuste cuadrático con pesos casi iguales. El ajuste acerca la solución de polyfit a un polinomio cuadrático.
• No existe ninguna pauta exacta para elegir el tramo. A medida que el tramo aumenta de tamaño, el gráfico del ajuste loess se suaviza, ya que se conectan menos tramos al ajuste. Sin embargo, es posible que el ajuste no siga las funcionalidades de datos correctamente. En cambio, a medida que el tramo disminuye de tamaño, es posible que loess no converja.
• El algoritmo loess no se ha diseñado para la extrapolación. Si intenta evaluar interp con valores que no se encuentran en el rango x original, se devolverá un error.
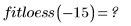
• Utilice loess cuando los datos tengan una característica algo discontinua, pero no desee realizar el ajuste por tramos manualmente, o bien utilice métodos de ajuste complejos, no realistas desde un punto de vista físico o no lineales.
Regresión polinomial multivariada
Utilice la función loess para realizar una regresión polinomial multivariada. Con la función loess no se pueden ajustar para más de cuatro variables independientes.
1. Defina un conjunto de datos.
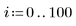
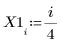
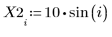
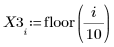
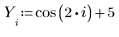
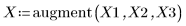
2. Defina un parámetro de suavizado.
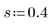
Este parámetro tiene el mismo significado que para el caso de un factor.
3. Llame a la función loess.
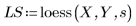
4. Llame a interp para interpolar funciones de ajuste multivariadas. La función de ajuste puede tomar un vector de n elementos o un conjunto de n argumentos, donde n es el número de factores independientes.
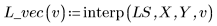
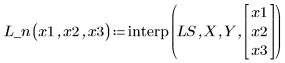
5. Utilice las funciones de ajuste para predecir el valor de Y en el punto (2, 3, 1).