Ejemplo: factorización de Cholesky de matrices complejas
Utilice la función Cholesky para realizar la factorización de Cholesky de una matriz Hermitian compleja.
|
|
Para evitar discrepancias lógicas al realizar comparaciones booleanas, active la opción Igualdad aproximada de la lista desplegable Opciones de cálculo.
|
1. Defina una matriz cuadrada definida Hermitian compleja M.
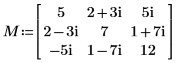
2. Aplique la función eigenvals para asegurarse de que la matriz sea definida positiva.
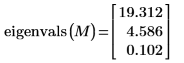
3. Defina los argumentos p y u para controlar la activación/desactivación del giro y la factorización inferior/superior.
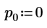 | 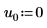 |
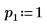 | 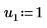 |
4. Utilice la función Cholesky para realizar la factorización por defecto de la matriz M, con giro y factorización inferior.

La función por defecto Cholesky(M) es equivalente a Cholesky(M,1,0). 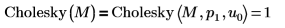 |
5. Muestre que P10T x M x P10 = L10 x conj(L10T).
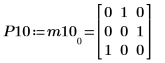 |  |
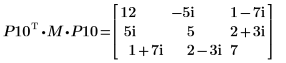 | 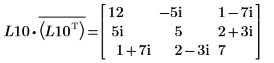 |
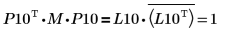 |
La relación es lógicamente verdadera.
6. Utilice la función Cholesky para realizar la factorización de la matriz M, sin giro y con factorización inferior (por defecto).

No especificar el argumento u, como en Cholesky(M, 0), equivale a definirlo en 0 como en Cholesky(M, 0, 0). 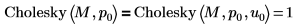 |
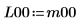
La matriz inferior devuelta, L10, cuando el giro está activado, no es igual a la matriz inferior devuelta, L00, cuando el giro está desactivado. 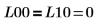 La relación es lógicamente falsa. |
7. Muestre que M = L00 x conj(L00T).
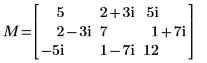 | 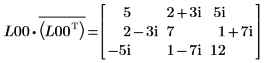 |
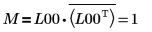 |
La relación es lógicamente verdadera.
8. Utilice la función Cholesky para realizar la factorización de la matriz M, con giro y factorización superior.
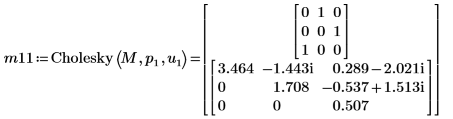 | |
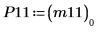 | 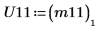 |
9. Muestre que P11T x M x P11 = conj(U11T) x U11.
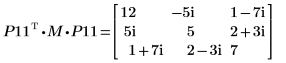 | 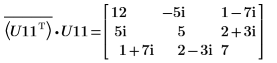 |
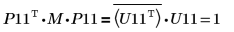 |
La relación es lógicamente verdadera.
10. Utilice la función Cholesky para realizar la factorización de la matriz M, sin giro y con factorización superior.

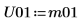
11. Muestre que M = conj(U01T) x U01.
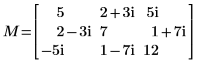 | 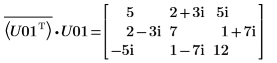 |
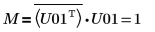 |
La relación es lógicamente verdadera.