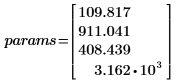Ejemplo: operador gradiente
• Defina una función f:
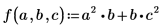
Utilice el operador gradiente para recibir un vector de derivadas parciales para f:
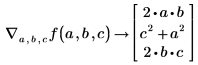
• Defina una función vectorial y calcule el gradiente de la función f por vector x.
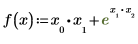

En este ejemplo, ORIGIN, que establece el índice inicial para todas las matrices, está definido como 0.
La variable con el mayor subíndice en f es x2. Mathcad asume que existen tres variables, x0, x1 y x2. El resultado es un vector de gradiente de tres valores que contiene las derivadas parciales de estas variables. Si x0 o x1 no han aparecido en f, Mathcad seguirá devolviendo un vector de tres valores, pero las entradas correspondientes a las variables faltantes se definirán como 0.
Para el mayor subíndice que aparece en f, n, Mathcad asume n + 1 variables, x0, x1, ... xn, y devuelve un vector de longitud n + 1.
• Si define x de forma numérica, puede evaluar el gradiente con el signo igual =. Mathcad evalúa el gradiente de los valores de x y devuelve un vector de números que representa el gradiente en el punto x. La longitud de x debe ser superior al mayor subíndice que aparece en f, y Mathcad devuelve un gradiente con entradas de longitud(x).
En el siguiente ejemplo, x0 y x1 son las únicas variables que aparecen en la expresión, por lo que Mathcad toma las derivadas parciales con respecto a x0 y x1, y devuelve un vector de dos valores.
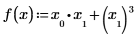
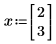
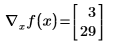
Sin embargo, si define x para que sea un vector de tres elementos, Mathcad asumirá que hay una variable adicional, x2, que no aparece en la expresión. El resultado es un vector de tres elementos.
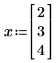
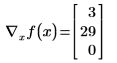
Uso del operador gradiente con la función genfit
El operador gradiente es especialmente útil para configurar los argumentos en la función genfit, que se ajusta a una función general y no lineal de un conjunto de datos.
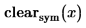
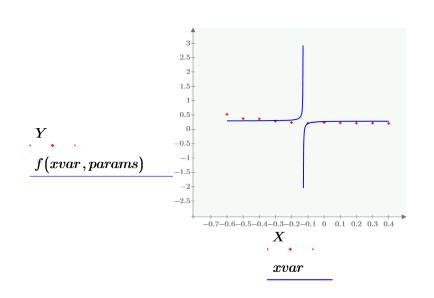
• Utilice los datos de la siguiente tabla.
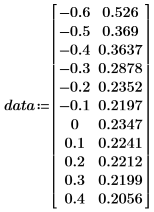
• La primera columna contiene los valores x de los datos, y la segunda columna incluye los valores y.
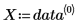
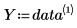
• Modele los datos mediante una función de la siguiente forma:
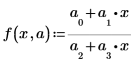
En este caso, a1, a2 y a3 son parámetros desconocidos contenidos en el vector a.
Puede modelar los datos llamando a genfit de la siguiente forma:
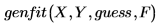
En esta expresión
◦ X e Y son vectores que contienen los valores x y los valores y de los datos.
◦ guess es un vector de valores de aproximación inicial de los parámetros.
◦ F es un vector cuya primera entrada es la función modelo f(x, a) y cuyas entradas restantes son las derivadas parciales de f con respecto a los parámetros desconocidos.
• Cree el vector F empleando el operador gradiente y la función stack.
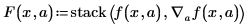

• La función stack coloca la función modelo f sobre el vector de derivadas parciales creado por el operador gradiente.
• A continuación, cree un vector de prueba para los parámetros.
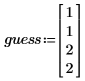
• Aplique genfit de la siguiente forma:
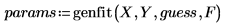
• Los parámetros que dan el resultado más adecuado son: